Császár Polyhedron 1

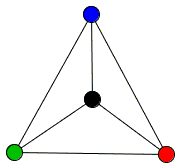
We are concerned here with a curious phenomenon of a polyhedron with no diagonals. Tetrahedron provides the simplest example. Its skeleton is the complete graph K₄.

Recollect the Euler polyhedral formula:

V - E + F = 2

which holds for simple polyhedrons.

Any polyhedron with no diagonals satisfies two conditions:

1. E = V(V - 1)/2,
2. 3F = 2E, because each of the faces is a triangle (lest there be a diagonal inside the face).

Substituting these into Euler's formula gives V - V(V - 1)/2 + V(V - 1)/3 = 2. The resulting quadratic equation has two roots V = 3 (the triangle with two faces - inside and outside) and V = 4 (the tetrahedron).

However there are other polyhedrons with no diagonals. These ones could not be simple. For the figures with h holes/tunnels the Euler formula has to be modified:

V - E + F = 2 - 2h.

However, regardless of the number of holes any figure with no diagonals is bound to satisfy the two properties above, thus again substituting the two but now into the extended Euler formula we obtain V - V(V - 1)/2 + V(V - 1)/3 = 2 - 2h. This gives a formula for h in terms of V, the number of vertices:

h = (V - 3)(V - 4)/12.

Now, for V = 3 and V = 4, h = 0 as it should. The next integer value for h is obtained with V = 7. For V = 7, E = 12(12 - 1)/2 = 21, F = 2·21/3, h = 1. This means a polyhedron with 7 vertices, 21 edges, 14 faces, and 1 hole. The latter means that, provided such a polyhedron exists, it is a toroid. This also means that the skeleton of such a polyhedron must be the complete graph K₇ on 7 vertices

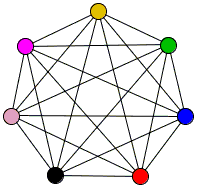
The polyhedron that answers all these requirement indeed exists and was discovered in the late 1940s by Ákos Császár [Gardner, p. 139-152].

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

What if applet does not run?

Drag the mouse to rotate the prism. Use the right button to remove and put back individual faces.

(Acknowledgement: I have learned most of Java details from the implementation by Meiko Rachimow. I found the geometry of the solid at the software3d online forum.)

References

1. M. Gardner, Time Travel and Other Mathematical Bewilderments, W.H.Freeman and Co., NY, 1988.

Related material Read more...
	Right Pentagonal Prism
	Square Pyramid
	Right Triangular Prism
	Twisted Triangular Prism
	Tetrahedron: an Interactive Model
	Octahedron: an Interactive Model
	Cube: an Interactive Model
	Icosahedron: an Interactive Model
	Dodecahedron: an Interactive Model
	Three Pyramids are Better Than Two
	Cube In Octahedron
	Octahedron In Cube
	Octahedron In Tetrahedron
	Tetrahedron In Cube
	Icosahedron In Cube
	Great Stellated Dodecahedron
	Lennes' Polyhedron
	Triangulated Dinosaur
	Volumes of Two Pyramids
	Császár Polyhedron 1
	Császár Polyhedron 4
	Szilassi Polyhedron
	Dissection of a Square Pyramid

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny