Three Pyramids are Better Than Two

The applet presents a tool for investigating an infamous problem. It showed up in 1980 as a practice problem on the Preliminary Scholastic Aptitude Exam, but, to an embarrassment of the Educational Testing Service, the marked answer was incorrect.

The problem is this [Winkler, p. 43]:

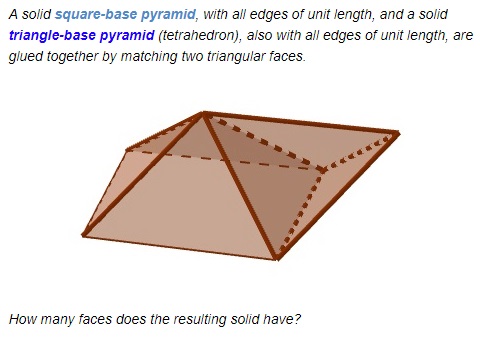
three pyramids, how many faces?, problem


No try playing with the GeoGebra applet below:


The expected solution was this. A square pyramid has 5 faces and a tetrahedron 4 faces. When two triangular faces are eliminated by gluing them together there remain 5 + 4 - 2 = 7 faces. By adding a second square-base pyramid, it becomes absolutely clear that, in the problem, there are two pairs of adjacent faces that align on a single plane (i.e., are coplanar) so that the resulting solid has two faces less than expected: 5 in all.

(As an aside, what is the relationship between the volumes of the square pyramid and the tertrahedron? Find out.

References

  1. P. Winkler, Mathematical Puzzles: A Connoisseur's Collection, A K Peters, 2004

Related material
Read more...

  • Right Pentagonal Prism
  • Square Pyramid
  • Right Triangular Prism
  • Twisted Triangular Prism
  • Tetrahedron: an Interactive Model
  • Octahedron: an Interactive Model
  • Cube: an Interactive Model
  • Icosahedron: an Interactive Model
  • Dodecahedron: an Interactive Model
  • Cube In Octahedron
  • Octahedron In Cube
  • Octahedron In Tetrahedron
  • Tetrahedron In Cube
  • Icosahedron In Cube
  • Great Stellated Dodecahedron
  • Lennes' Polyhedron
  • Triangulated Dinosaur
  • Volumes of Two Pyramids
  • Császár Polyhedron 1
  • Császár Polyhedron 4
  • Szilassi Polyhedron
  • Dissection of a Square Pyramid

    • |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    72111711