Simultaneous Diameters in Concurrent Circles

What is this about?
A Mathematical Droodle

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny

The applet attempts to suggest the following problem [Geometry, p. 258]:

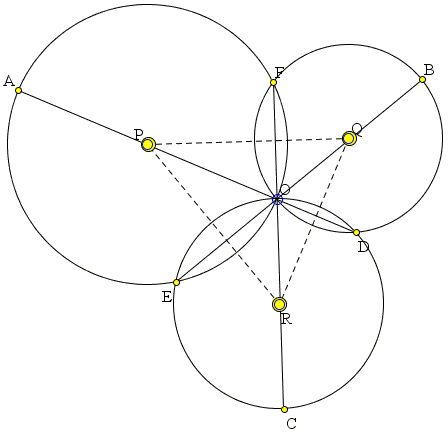
Three circles, say, (P), (Q), (R), concur at point O, and meet at three other points D, E, and F, as illustrated in the applet. The following sets of points are collinear: A, O, D; B, O, E; C, O, F. OA is a diameter of (P); OB is a diameter of (Q). Prove that OC is a diameter of (R).

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

Proof 1

Invert the diagram in a circle with center O. Circles (P), (Q), (R) map onto straight lines that form a triangle with vertices D', E', F' which are respective images of D, E, F. Lines AD, BE, CF that pass through the center O of inversion map onto themselves and thus serve cevians in ΔD'E'F' that concur at O.

Every diameter in a circle is perpendicular to a circle, i.e., to the tangents at its endpoints. Thus, e.g., AD ⊥ (P). Due to the angle presevation property of inversion, D'A' ⊥ E'F', meaning that D'A' is an altitude in ΔD'E'F'. The same of course holds for E'B'. The two altitudes D'A' and E'B' in ΔD'E'F' meet at the orthocenter O which shows that the third cevian - F'C' - is also an altitude. As such, F'C' ⊥ D'E', while their inverse images, i.e., FC and (R) are also perpendicular. Thus, OC is indeed a diameter of (R).

Proof 2

Let A' lie on (P) in an arc EF that does not contain O. Define B' as the second intersection of A'F with (Q), and C' as the second intersection of A'E with (R). We know that B'C' pass through D. Furthermore, position of A' does not affect the angles in ΔA'B'C', so that all those triangles are similar. One of these triangles is the largest. This is the triangle for which OA', OB', OC' are the diameters of (P), (Q), and (R), respectively. In fact, if one of them is a diameter, so are the other two.

We are in fact given that, for A' = A, B' = B. We need to show that then C' = C.

Since OA is a diameter of (P), ∠AEO = 90°. Since OB is a diameter of (Q), ∠BDO = 90°, implying that in ΔABC', AD and BE are altitudes, O the orthocenter, and C'O is the thrid altitude. But, since OA is a diameter of (P), OF ⊥ AB, and thhus F belongs to C'O. But FO has just one other (besides O) intersection with (R) and so C = C'.

Proof 3

This proof has been devised by Patrick Honner and relates to the following diagram:

I placed the proof on a separarte page.

Proof 4

The problem admits a generalization: instead of the common chords, we may consider the radical axes of two circles. Such a generalization is indeed valid and is treated on a separate page. The concurrency of the circles appears to be a red herring.

References

1. D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002

Inversion - Introduction

• Angle Preservation Property
• Apollonian Circles Theorem
• Archimedes' Twin Circles and a Brother
• Bisectal Circle
• Chain of Inscribed Circles
• Circle Inscribed in a Circular Segment
• Circle Inversion: Reflection in a Circle
• Circle Inversion Tool
• Feuerbach's Theorem: a Proof
• Four Touching Circles
• Hart's Inversor
• Inversion in the Incircle
• Inversion with a Negative Power
• Miquel's Theorem for Circles
• Peaucellier Linkage
• Polar Circle
• Poles and Polars
• Ptolemy by Inversion
• Radical Axis of Circles Inscribed in a Circular Segment
• Steiner's porism
• Stereographic Projection and Inversion
• Tangent Circles and an Isosceles Triangle
• Tangent Circles and an Isosceles Triangle II
• Three Tangents, Three Secants
• Viviani by Inversion
• Simultaneous Diameters in Concurrent Circles

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny