Three collinear Circles and Simultaneous Diameters

Here we add a third proof to a problem addressed elsewhere:

Three circles centered at P, Q, R are concurrent at O and also meet pairwise at points D, E, and F.

three collinear circles and simultaneous diameters

Assume D, O, P are collinear and so are E, O, Q. Then F, O, R are also collinear.

Proof

This proof is due to Patrick Honner, a high school math teacher from New York.

The center lines PQ, QR, PR of the three circles are the perpendicular bisectors of the three common chords: FO, DO, and EO, respectively.

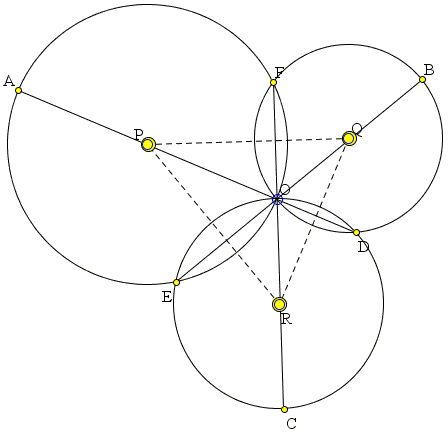
three concurrent circles and simultaneous diameters

Assume, as stipulated in the problem, that P lies on the extension of OD and Q on the extension of OE. In ΔPQR, PD ⊥ QR and QE ⊥ PR. In other words, PD and QE are two altitudes in ΔPQR. This makes O its orthocenter and OR the third altitude. However, as we've mentioned, PQ is a perpendicular bisector of FO, so that FO ⊥ PQ. Now, since also OR ⊥ PQ (and there is only one perpendicular to PQ through O), the three points F, O, R are collinear, as required.

This proof points to a possible generalization of the problem: instead of the common chords, we may consider the radical axes of two circles. Such a generalization is indeed valid and is treated on a separate page.

71925312