A Property of Points on Incircle

Introduction and acknowledgment

Miguel Ochoa Sanchez (Peru) has posted an intriguing problem on top of a beautiful picture that I was forced to bespoil due to formatting requirements:

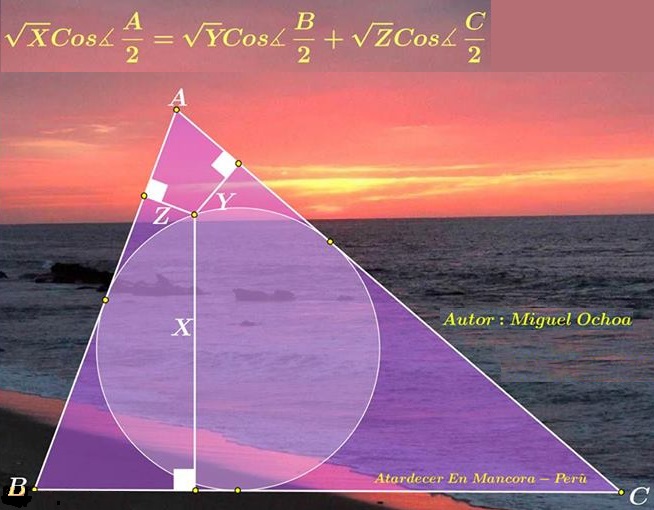
Point on incircle - problem

Miguel also posted an elegant solution that is reproduced below.

Problem

$P$ is a point on the incircle of $\Delta ABC,$ $x,y,z$ its distances to the sides $BC,$ $AC,$ and $AB,$ respectively. If vertex angles are denoted by the same letters as the vertices, and $x$ is the longest of the three segments, then

$\displaystyle\sqrt{x}\cos\frac{A}{2}=\sqrt{y}\cos\frac{B}{2}+\sqrt{z}\cos\frac{C}{2}.$

Solution

The proof depends on the following

Lemma

Let $M$ be a point on a line tangent to circle $(O)$ with radius $R$ at point $N.$ $T$ a point on the circle such that $MT\perp MN.$ Denote $w=MT.$

Point on incircle - lemma

Then $TN=\sqrt{2Rw}.$

Proof of Lemma

Drop perpendicular $TS$ onto $ON.$

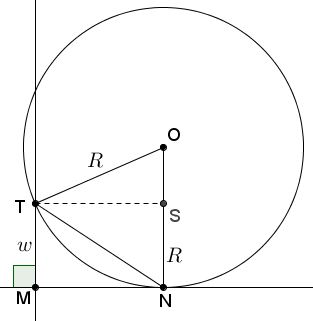
Point on incircle - lemma, solution

In $\Delta MNT,$ $TN^{2}=w^{2}+MN^{2}.$ In $\Delta OST,$ $TS^{2}=R^{2}-(R-w)^{2}=2Rw-w^{2}.$ Combining the two,

$\begin{align} TN^{2}&=w^{2}+MN^{2}\\ &=w^{2}+TS^{2}\\ &=w^{2}+(2Rw-w^{2})\\ &=2Rw, \end{align}$

as required.

Proof of Statement

According to Lemma, $FP=\sqrt{2Rz},$ $PE=\sqrt{2Ry},$ $PD=\sqrt{2Rx}.$

In $\Delta DOE,$ $\displaystyle DE=2R\cos\frac{C}{2}.$ Similarly, $\displaystyle FD=2R\cos\frac{B}{2}$ and $\displaystyle FE=2R\cos\frac{A}{2}.$

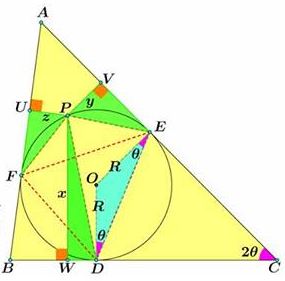Point on incircle - solution>
</p>

<p>By <a href= Ptolemy's theorem in the quadrilateral $FPED,$ $PD\cdot FE=PE\cdot FD+FP\cdot DE.$ Substituting the above,

$\displaystyle\sqrt{2Rx}\cdot 2R\cos\frac{A}{2}=\sqrt{2Ry}\cdot 2R\cos\frac{B}{2}+\sqrt{2Rz}\cdot 2R\cos\frac{C}{2},$

and, after simplification

$\displaystyle\sqrt{x}\cos\frac{A}{2}=\sqrt{y}\cos\frac{B}{2}+\sqrt{z}\cos\frac{C}{2}.$

Ptolemy's Theorem

71930845