Sides and Area of Pedal Triangle

Pedal triangle of point $P$ with respect to a given $\Delta ABC$ is formed by the feet of the perpendiculars from $P$ to the sides of $\Delta ABC.$ The most popular of these is, probably, the orthic triangle obtained when $P=H,$ the orthocenter of $\Delta ABC.$ For points $P$ on the circumcircle $(ABC),$ the pedal triangle degenerates into what is known as the Simson line, or just a simson.

Below I shall derive several formulas relating the elements of general pedal triangle to those of the base triangle $ABC.$

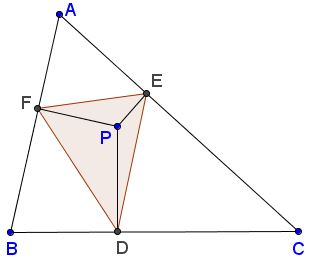
Pedal triangle

One property is the consequence of the fact that the pedal points $D,E,F,$, vertices $A,B,C,$ and point $P$ itself lie on three circles, $(AFPE)$ being one of them. The angle $\alpha$ at the vertex $A$ is an inscribed angle in two circles: $(ABC)$ and $(AFPE).$ Note that in the latter $AP$ is a diameter.

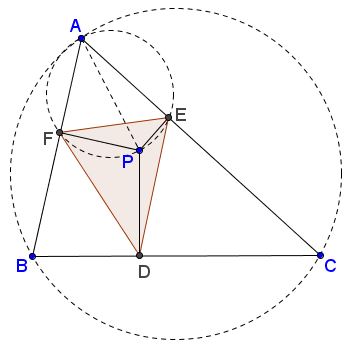
Pedal triangle - sides

By the Law of Sines, $BC=2R\sin\alpha$ and $EF=AP\sin\alpha,$ where $R$ is the circumradius of $\Delta ABC.$ It follows that

$\displaystyle EF=\frac{AP\cdot BC}{2R}.$

Similarly, $DE=CP\cdot AB/ 2R$ and $DF=BP\cdot AC/ 2R.$

Now, let $BP$ meet $(ABC)$ second time in $B'.$

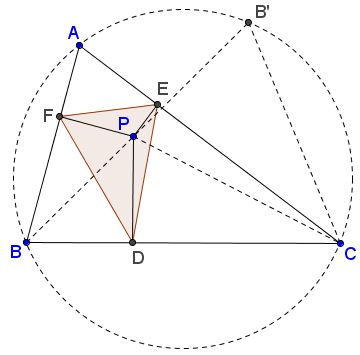
Pedal triangle - area

Further, on one hand, by angle chasing, $\angle BPC=\angle BAC+\angle EDF.$ Indeed,

$\begin{align} \angle BPC &= 360^{\circ} -\angle BPF-\angle FPA-\angle APE-\angle EPC\\ &=360^{\circ} - (180^{\circ}-\angle FAE) - \angle BDF - \angle EDC\\ &= 180^{\circ} + \angle BAC - (180^{\circ}-\angle EDF)\\ &= \angle BAC+\angle EDF. \end{align}$

On the other hand, by the Exterior Angle Theorem,

$\begin{align} \angle BPC &=\angle PB'C+\angle B'CP\\ &=\angle BB'C+\angle B'CP\\ &=\angle BAC+\angle B'CP. \end{align}$

We may thus conclude that $\angle EDF=\angle B'CP.$

so that $\angle EDF=\angle B'CP.$

Let now $[X]$ denote the area of shape $X,$ $\beta =\angle ABC,$ $\gamma =\angle ACB.$ Then

$\begin{align} [\Delta EDF] &= \frac{1}{2}DE\cdot DC\cdot \sin\angle EDF\\ &= \frac{1}{2}DE\cdot DF\cdot \sin\angle B'CP\\ &= \frac{1}{2}CP\sin\gamma\cdot BP\sin\beta\cdot \sin\angle B'CP. \end{align}$

But $\displaystyle\frac{B'P}{\sin\angle B'CP}=\frac{CP}{\sin\angle BB'C}=\frac{CP}{\sin\alpha }.$ It follows that

$\begin{align} [\Delta EDF] &= \frac{1}{2}BP\cdot B'P\cdot \sin\alpha\sin\beta\sin\gamma\\ &= \frac{1}{2}(R^{2}-OP^{2})\cdot \sin\alpha\sin\beta\sin\gamma \\ &= \frac{1}{2}(R^{2}-OP^{2})\cdot \displaystyle\frac{abc}{(2R)^{3}}\\ &= \frac{1}{2}(R^{2}-OP^{2})\cdot \displaystyle\frac{[\Delta ABC]}{2R^{2}}\\ &= \frac{1}{4}(R^{2}-OP^{2})\cdot \frac{[\Delta ABC]}{R^{2}}, \end{align}$

where $O$ is the circumcenter of $\Delta ABC$ and where I used a known identity $4R[\Delta ABC]=abc.$

Observe, as a consequence, we get another proof of the existence of simson lines. For points $P$ on the circumcircle, $OP=R$ so that $[\Delta EDF]=0,$ meaning that the three points are collinear.

References

R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 1960, 135-141

72204528