As a more serious example, let’s take the case of a triangle inside a semicircle:

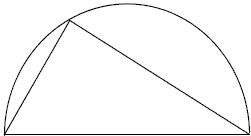
Now the beautiful truth about this pattern is that no matter where on the circle you place the tip of the triangle, it always forms a nice right angle. (I have no objection to a term like “right angle” if it is relevant to the problem and makes it easier to discuss. It’s not terminology itself that I object to, it’s pointless unnecessary terminology. In any case, I would be happy to use “corner” or even “pigpen” if a student preferred.)

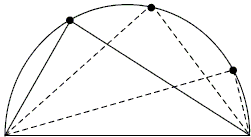
Here is a case where our intuition is somewhat in doubt. It’s not at all clear that this should be true; it even seems unlikely— shouldn’t the angle change if I move the tip? What we have here is a fantastic math problem! Is it true? If so, why is it true? What a great project! What a terrific opportunity to exercise one’s ingenuity and imagination!

...

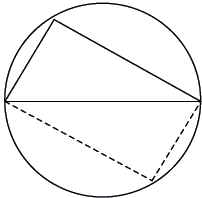
Take the triangle and rotate it around so it makes a foursided box inside the circle. Since the triangle got turned completely around, the sides of the box must be parallel, so it makes a parallelogram. But it can’t be a slanted box because both of its diagonals are diameters of the circle, so they’re equal, which means it must be an actual rectangle. That’s why the corner is always a right angle.

...

(AB: note that) Since the triangle got rotated halfway around the circle, the tip must end up exactly opposite from where it started. That’s why the diagonal of the box is a diameter.