Looking Back at Bottema

What Might This Be About?

Problem

Given $\Delta ABC$ and point $V$ on its circumcircle $(ABC).$ Draw circle $C(A)$ through $C$ with center $A$ and, similarly defined circle $C(B).$ Let the ray from $V$ through $A$ meet $C(A)$ in $F$, and that from $V$ through $B$ meet $C(B)$ at $G.$

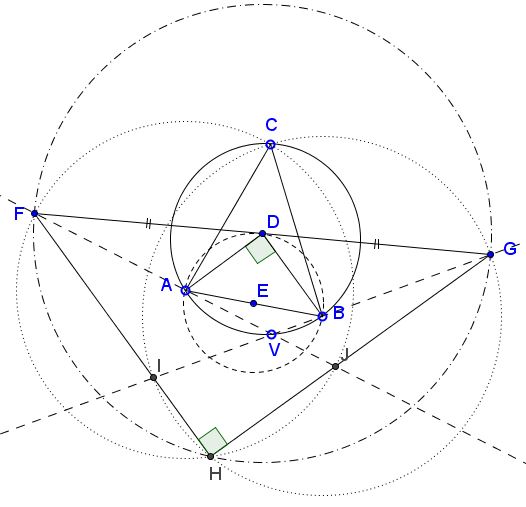
A configuration related to Bottema's theorem

Then

  1. $D,$ the midpoint of $FG,$ lies on the circle with diameter $AB$ so that $\angle ADB=90^{\circ},$

  2. $D$ is independent of the position of $C$ if, when $C$ moves, $V$ is chosen to preserve angles $FAC$ and $GBC.$

  3. If $H$ is the second intersection of $C(A)$ and $C(B)$ then $\angle FHG=90^{\circ},$ so that $H$ also lies on the circle with diameter $FG,$

  4. Point $I$ the intersection of $VB$ and $FH$ lies on $C(B)$ and similarly defined $J$ lies on $C(A).$

Solution

Quadrilateral $AVBC$ is cyclic, implying that angles $CBV$ and $CAV$ are supplementary, .i.e., $\angle CBV+\angle CAV=180^{\circ}.$ By the construction, so are angles $CAV$ and $CAF$ and also $CBV$ and $CBG,$ implying that angles $CAF$ and $CBG$ are supplementary, which, with a reference to a generalization of Bottema's theorem, shows that $\angle ADB=90^{\circ}$ such that $D$ lies on the circle with diameter $AB.$

But this is also possible toestablish #1 directly, without invoking the generalization of Bottema's theorem and, thus providing an alternative (and purely synthetic) proof of the latter. Indeed, due to Thales' theorem, the parallel to $GH$ through $A$ meets $FG$ at its midpoint $D$ but $BD$ is parallel with $FH$ therefore $\angle ADB$ is right and $D$ is on the circle with diameter $AB,$ as required.

Let $I$ be the point where $GB$ meets $C(B)$ again and let $H$ be where $FI$ meets $C(B)$ again. Since $BI$ is a diameter of $C(B),$ $\angle IHG=90^{\circ}.$ Since $\angle FHG=90^{\circ},$ the intersection $J$ of $HG$ with $C(A)$ must be its diameter, $H$ must be on $C(A)$ and $FG$ must be the diameter of $(FGH).$

Acknowledgment

The appearance of point $V$ in the setup of the generalization of Bottema's theorem is due to Hubert Shutrick's insight that the generalization could be formulated without invoking rotations; points $I,J,H$ emerged in a follow-up investigation; their properties proved by Hubert Shutrick.

Bottema's Theorem

  1. Bottema's Theorem
  2. An Elementary Proof of Bottema's Theorem
  3. Bottema's Theorem - Proof Without Words
  4. On Bottema's Shoulders
  5. On Bottema's Shoulders II
  6. On Bottema's Shoulders with a Ladder
  7. Friendly Kiepert's Perspectors
  8. Bottema Shatters Japan's Seclusion
  9. Rotations in Disguise
  10. Four Hinged Squares
  11. Four Hinged Squares, Solution with Complex Numbers
  12. Pythagoras' from Bottema's
  13. A Degenerate Case of Bottema's Configuration
  14. Properties of Flank Triangles
  15. Analytic Proof of Bottema's Theorem
  16. Yet Another Generalization of Bottema's Theorem
  17. Bottema with a Product of Rotations
  18. Bottema with Similar Triangles
  19. Bottema in Three Rotations
  20. Bottema's Point Sibling

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

71867322