Some Properties of Napoleon's Configuration

Napoleon's theorem claims that the centers $A', B', C',$ of the equilateral triangles $A''BC,$ $AB''C,$ $ABC'',$ erected on the sides of a given triangle $ABC$ form an equilateral triangle. This is true if the triangles $A''BC,$ $AB''C,$ $ABC'',$ are constructed "outwardly":

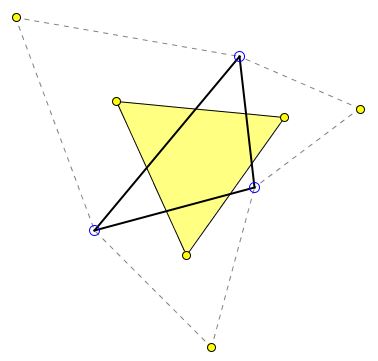
(outer) Napoleon triangles

and also when they are constructed "inwardly":

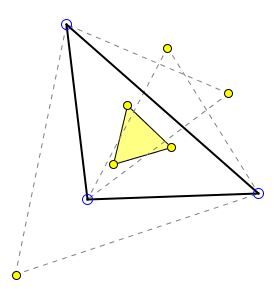
(inner) Napoleon triangles

The corresponding triangles are known as the outer and, respectively, inner, Napoleon triangles. The properties of one parallel the properties of the other, and there are also properties they have as a pair.

First Property

The centroid of Napoleon's triangle $A'B'C'$ coincides with that of the reference triangle ABC.

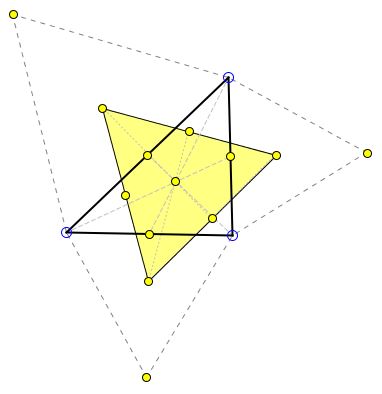
centroids of the Napoleon and reference triangles coincide

The simplest proof I am aware of makes use of complex numbers, see a separate discussion. The proof holds both for the outer and the inner Napoleon's triangles. It follows that the centroids of the two Napoleon triangles - the outer and the inner - coincide. This fact was mentioned in the classical [Geometry Revisited, p. 65], [Complex Numbers and Geometry, p. 113] or [MathematicalGems, p. 40]. The two books, however, failed to mention that the same point also serves as the centroid of the base triangle $ABC.$

Second Property

Lines $AA'',$ $BB'',$ $CC''$ meet in a point - one (either inner or outer) of Fermat's points of $\Delta ABC.$

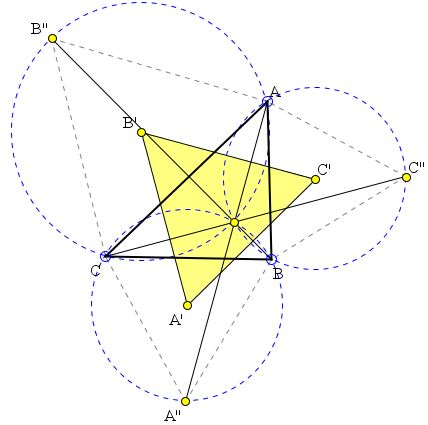
Fermat's point in Napoleon's configuration

The three lines form equal angles of $60^{\circ}$ or $120^{\circ},$ depending on how one looks at the configuration. This is equivalent to the claim that the circumcircles of triangles $ABC'',$ $AB''C,$ and $A''BC$ are concurrent.

This implies the next property.

Third Property

The sides of the Napoleon triangle serve as perpendicular bisectors of the lines joining Fermat's point to the vertices of $\Delta ABC.$

This follows from the fact that, by the construction, the vertices of Napoleon's triangle are the centers of the circumcircles of triangles $ABC'',$ $AB''C,$ and $A''BC$ while the segments $AF,$ $BF,$ $CF$ ($F$ being the Fermat point) are the common chords of the circles taken two at a time.

Fourth Property

The circumcricles of Napoleon's triangles are concurrent; in an acute triangle they meet at Fermat's point. As such, they admit a triangle with one vertex on each of the circles whose sides pass through the vertices of the base triangle.

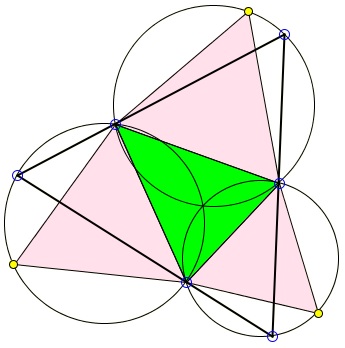
porism in Napoleon's configuration

This is actually a porism: the starting point for the construction of that triangle can be chosen arbitrarily. The triangle is always equilateral.

Fifth Property

Here we deal with both inner and outer Napoleon's triangles. This necessitates notations that differentiate between the two.

Let $ABC_{o},$ $BCA_{o},$ $CAB_{o}$ be the outer, $ABC_{i},$ $BCA_{i},$ $CAB_{i}$ the inner Napoleon's triangles.

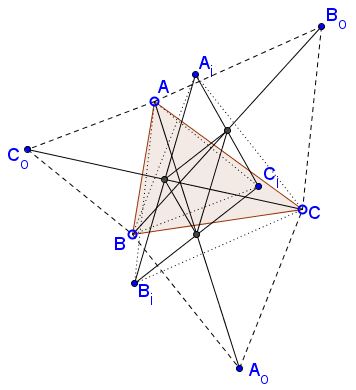
Napoleon's configuration - passing through the midpoints

Then the midpoints of $AA_{o}$ and $B_{i}C_{i}$ coincide as are the midpoints of $BB_{o},$ $C_{i}A_{i}$ and $CC_{o},$ $A_{i}B_{i}.$ A similar assertion holds with the exchange of the indices $_{o}$ and $_{i}$ throughout.

For proof see a separate page.

Sixth Property

Here we return to the previous notations for Napoleon's triangles $A''BC,$ $AB''C,$ $ABC''$ and their centroids $A',$ $B',$ and $C',$ respectively.

Let $K_A,K_B,K_C$ be the centroids of triangles $AB''C'',A''BC'',A''B''C,$ respectively.

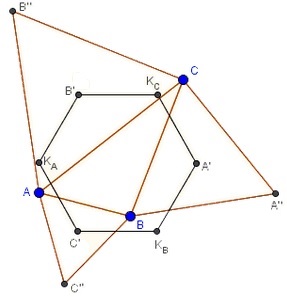
Napoleon's hexagon

Then the hexagon $A'K_CB'K_AC'K_B$ is regular.

Seventh Property

Form equilateral triangles $ABC'',\;$ $AB''C,\;$ $A''BC\;$ on the sides of $\Delta ABC\;$ and define $D = \frac{1}{2}(A''+B'')\;$ and $E=\frac{1}{2}(A''+C'').$

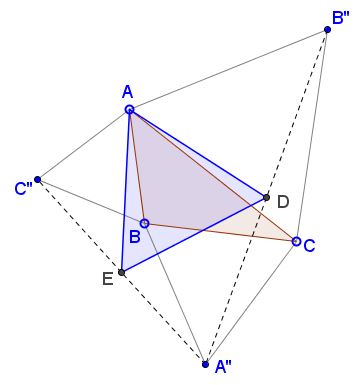
another equilateral triangle in Napoleon's configuration

Prove that $\Delta ADE\;$ is equilateral.

For a proof see a separate page.

References

H. S. M. Coxeter, S. L. Greitzer, Geometry Revisited, MAA, 1967
Liang-shin Hahn, Complex Numbers & Geometry, MAA, 1994
R. Honsberger, Mathematical Gems, MAA, 1973

Napoleon's Theorem

71534218