The Fermat Point and Generalizations
P. Fermat (1601-1665) challenged Evangelista Torricelli(*) (1608-1647), the inventor of barometer with the following question
Find the point such that the sum of its distances from the vertices of a triangle is a minimum.
Torricelli presented several solutions. In one he observed that the circumcircles of the equilateral triangles constructed externally on the sides of a given triangle meet in a point. Many more have been found since. I'll present several solutions and two quite surprising generalizations.
Solution 1
(Published by Joseph Ehrenfried Hofmann (1900--1973) in 1929. It was independently discovered by Tibor Galai and others [Honsberger, p. 26].)
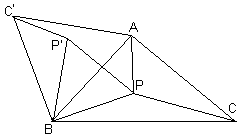
In $\Delta ABC,$ select point $P$ and connect it with vertices $A,$ $B,$ and $C.$ Rotate $\Delta ABP$ $60^{\circ}$ around $B$ into position $C'BP'.$ By construction, $\Delta BPP'$ is equilateral, $PB = P'B,$ and $PA = C'P'.$ We thus have $PA + PB + PC = C'P' + P'P + PC.$ As the image of $A$ under the rotation, position of $C'$ does not depend on $P.$ Also, $PA + PB + PC \ge CC'$ because the broken line $CPP'C'$ is no shorter than the straight line $CC'.$ Therefore, $PA+PB+PC$ reaches its minimum iff $P$ lies on $CC'.$ For this P, $\angle BPC' = 60^{\circ}.$ Had we rotated $\Delta ABP$ around $A,$ we would have found that $\angle APC' = 60^{\circ}.$
The result is clearly related to Napoleon's theorem. On the sides of $\Delta ABC$ construct equilateral triangles $ABC',$ $ACB',$ and $BCA'.$ We know that the Fermat point $P$ that minimizes the sum $PA + PB + PC$ lies on $CC'.$ By the same token, it lies on $AA'$ and $BB'.$ Therefore, it lies on their intersection. As far as Napoleon's theorem goes, the three lines $AA',$ $BB',$ and $CC'$ are concurrent. (This was already known to Thomas Simpson (1710-1761).) Not only that but they cross at angles equal $120^{\circ}.$ Furthermore, $AA' = BB' = CC'$ since each of them equals $PA + PB + PC$ for the Fermat point $P.$
So the Fermat point is unique and lies at the intersection of three straight lines that connect vertices of the triangle with opposite vertices of Napoleon's triangles. The construction fails if one of the internal angles of $\Delta ABC$ is $120^{\circ}$ or more. In this case, the vertex corresponding to the largest angle of the triangle solves Fermat's problem.
(There is a dynamic illustration pertinent to the above proof.)
Solution 2
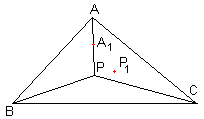
This solution only works under the assumption that the Fermat point exists and is unique. Let for a given $\Delta ABC,$ $P$ be that point. Let's move, say, $A$ a little into position $A_{1}$ on the ray $PA.$ Will $P$ move along into a different position? Assuming it will and denoting its new position as $P_{1},$ we arrive at contradiction. Indeed, for $\Delta ABC,$
$PA + PB + PC < P_{1}A + P_{1}B + P_{1}C.$
Also, by our assumption for $\Delta A_{1}BC,$
$P_{1}A_{1} + P_{1}B + P_{1}C \lt PA_{1} + PB + PC.$
Summing up and cancelling, we get
$PA + P_{1}A_{1} \lt PA_{1} + P_{1}A.$
Recollect that we selected $A_{1}$ on the ray $PA$ so that $PA_{1} + A_{1}A = PA.$ Which leads to
$AA_{1} + P_{1}A_{1} \lt P_{1}A$
which is of course absurd. Therefore, when $A$ slides along the ray $PA,$ point $P$ does not change. Slide then vertices $A$ and $B$ so as to make $\Delta ABC$ equilateral. This is always possible. For example, start with sliding $A$ so as to make $AB = BC.$ The triangle $ABC$ becomes isosceles. It is obvious that, for an isosceles triangle, the Fermat point lies on the axis of symmetry of the triangle. For this reason, the triangle remains isosceles wherever $B$ is located on that axis. Slide it so as to make all three sides of $\Delta ABC$ equal. For an equilateral triangle, its centroid that also serves as the incenter and the circumcenter, serves as the Fermat point as well.
In other words, since the line segments joining the Fermat point to the vertices of an equilateral triangle form $120^{\circ}$ angles, the same holds for any triangle for which Fermat point exists.
Solution 3
([Honsberger, p. 26] ascribes this solution to Torricelli himself and mentions that it was rediscovered almost 300 years later by F. Riesz. In a private communication, Douglas Rogers mentioned that the solution has been also proposed by J. Steiner. Thus the same object that is most frequently referred to as Fermat's point, Torricelli's point and Fermat-Torricelli point, is sometimes also named after J. Steiner, as Steiner's point, especially in the framework of Steiner's networks. [Tikhomirov, p. 31] and [Courant and Robbins, p. 354] even refer to Fermat's problem as Steiner's. [Johnson, p. 221] attributes the present solution to Steiner.)
The following solution depends on explicit knowledge of the fact that, for Fermat's point $F,$ $\angle AFB = \angle BFC = \angle AFC = 120^{\circ}.$ Without proving that such a point exists, it shows that, if it does, it solves Fermat's problem.
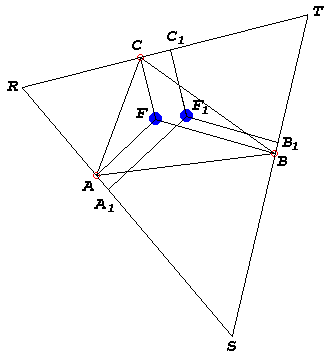
At the vertices of $\Delta ABC$ draw perpendiculars to lines $AF,$ $BF,$ and $CF.$ The new lines form an equilateral triangle $RST.$ Let $F_{1}$ be a point different from $F.$ Drop perpendiculars $F_{1}A_{1},$ $F_{1}B_{1}$ and $F_{1}C_{1}$ to the sides of $\Delta RST.$ It's a nice property (known as Viviani's theorem) of equilateral triangles that in $\Delta RST,$
$FA + FB + FC = F_{1}A_{1} + F_{1}B_{1} + F_{1}C_{1}.$
(The sum of the distances from a point inside an equilateral triangle to the sides of the triangle does not depend on the point. )
On the other hand, obviously,
$F_{1}A_{1} + F_{1}B_{1} + F_{1}C_{1} < F_{1}A + F_{1}B + F_{1}C.$
All that remains is to combine the two.
(Douglas Rogers made a delightful observation. $\Delta RST$ is the largest equilateral triangle circumscribing $\Delta ABC.$ According to Viviani's theorem, $FA,$ $FB,$ $FC$ add up to the altitude of $\Delta RST.$ For any other equilateral $\Delta LMN$ circumscribing $\Delta ABC,$ at least one of $FA,$ $FB,$ or $FC$ is not perpendicular to the side and hence is longer than such perpendicular. It follows that the sum $FA + FB + FC$ is bound to be larger than the altitude of $\Delta LMN.$ This implies that the side of $\Delta LMN$ is smaller than that of $\Delta RST.$ In passing, $\Delta RST$ is known as the antipedal triangle of $F$ with respect two $\Delta ABC.)$
Solution 4
(The proof by Lou Talman is found on one of the discussions at the mathforum. Still very simple, it uses a little bit of analytic geometry and calculus. This is probably very close to one of Torricelli's original proofs.)
One can see that the Fermat point does minimize $FA + FB + FC$ as follows: Let $z$ be the sum $FA + FB,$ where $F$ is chosen to minimize $FA + FB + FC,$ and consider the locus of points $P$ that satisfy $PA + PB = z.$ This locus is an ellipse with foci at $A$ and $B.$ Because $F$ minimizes $z + FC,$ the line determined by $C$ and $F$ must be normal to the tangent to this ellipse at $F.$ By the reflection property of the ellipse, the angles $AFC$ and $BFC$ must be equal. A similar argument shows that the angles $AFC$ (say) and $AFB$ must also be equal. From this it follows that the three angles are all $120^{\circ}.$
Solution 5
(The argument is similar to that in Solution 4, but from a different perspective. [F. G.-M., p. 442] credits Lhuilier (1811) with the proof.)
Assume $FC$ is constant. Then point $F$ that minimizes $FA + FB + FC$, minimizes also $FA + FB$ and lies on the circle with center $C$ and radius $FC.$ The minimum is achieved for a point $F$ on the circle for which the angles $AFC$ and $BFC$ are equal.
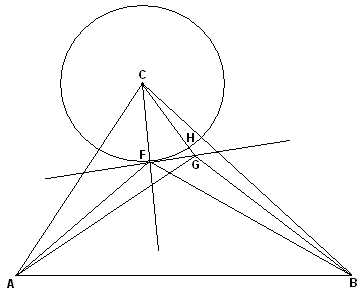
For more detail, draw a tangent to the circle at $F$ and choose any point $G$ on the tangent other than $F.$ Let $H$ be the intersection of $HC$ with the circle. Then, assuming angles $AFC$ and $BFC$ equal,
$FA + FB \lt GA + GB \lt HA + HB.$
(The latter inequality warrants extra attention. It follows from the fact the various ellipses with foci at $A$ and $B$ do not intersect.) From here,
$FA + FB + FC \lt HA + HB + FC = HA + HB + HC.$
The argument can be repeated assuming either $FA$ or $FB$ constant. As a result, at Fermat's point $F$ all three angles $AFC,$ $BFC$ and $AFB$ are found to be equal.
Solution 6
Fermat's point can be located with the help of Euler's generalization of Ptolemy's Theorem, see [Pedoe, pp. 93-94].

Any triangle has at least two acute angles. Given $\Delta ABC,$ let angles at $B$ and $C$ be acute. Form an equilateral triangle $BCD,$ with $D$ and $A$ on opposite sides of $BC.$ Let $(O)$ be the circumcircle of $\Delta BCD.$
For a point $Q,$ by Ptolemy's inequality
$BQ\cdot CD + CQ\cdot BD \ge DQ\cdot BC,$
with equality only if $Q$ lies on $(O)$ and such that the quadrilateral $BQCD$ is convex. Note that, by construction, $BC = CD = BD$ which reduces the above to
$BQ + CQ \ge DQ.$
Therefore
$AQ + BQ + CQ \ge AQ + DQ \ge AD.$
Unless $Q$ lies on $AD,$ $AQ + BQ + CQ \gt AD.$ Let $P$ be the intersection of $AD$ with $(O)$ other than $D.$ $BPCD$ is an inscribed convex quadrilateral and $P$ lies on $AD.$ So in this (and only in this) case $AP + BP + CP = AD.$ For any other selection of $Q,$
$AQ + BQ + CQ \gt AP + BP + CP.$
Angle $BPC$ is supplementary to $\angle BDC = 60^{\circ}$ so that $\angle BPC = 120^{\circ}.$ Further, $D$ is in the middle of the arc $BDC$ so that angles $BPD$ and $CPD$ are both $60^{\circ},$ making angles $APC$ and $APB$ both equal $120^{\circ}.$
If the triangle is acute the same construction applies to the other two sides which brings up the framework of Napoleon's theorem. The three circles intersect at Fermat's point and three lines joining the vertices of $\Delta ABC$ with the opposite vertices of the Napoleon triangles concur at the point P.
The latter fact can be used for a more direct proof.
Solution 7
(This was a part of a solution by Grimbal to a problem posted at the wu::forum.)
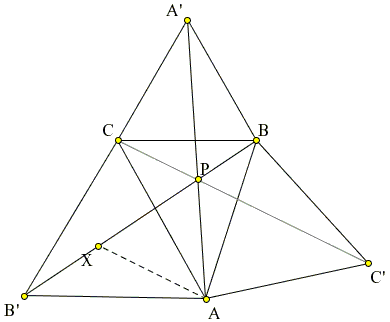
Construct Napoleon's equilateral triangles $ABC',$ $AB'C',$ $A'BC$ externally on the sides of $\Delta ABC.$ Let $P$ be the intersection of $AA'$ and $BB'.$ $AA'$ is $CC'$ rotated clockwise $60^{\circ}$ about $B,$ and $BB'$ is $CC'$ rotated counterclockwise $60^{\circ}$ about $A,$ it follows that angle $APB'$ is $60^{\circ}.$ Let $X$ be the point on $BB'$ making triangle $APX$ equilateral. Now, if $BB'$ is rotated clockwise $60^{\circ}$ about $A,$ then $X$ goes to $P,$ $B'$ to $C,$ and $B$ to $C'.$ Hence $P,$ $C,$ and $C'$ are collinear; and so $AA',$ $BB',$ and $CC'$ are concurrent, and any two of these lines make an angle of $120^{\circ}.$
A most elegant solution in complex numbers can be found elsewhere.
Searching for the Fermat point we discovered a nice property of Napoleon's triangles. I found quite surprising generalizations of those properties in a column by David Gale in The Mathematical Intelligencer which was kindly pointed out to me by Professor McWorter.
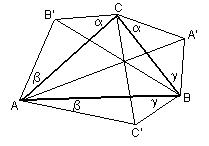
Two lines passing through a vertex of a triangle are called isogonal with respect to that vertex if they form equal angles with its (internal) angle bisector. Following is the first generalization.
Theorem 1
As in the diagram, assume lines $AB'$ and $AC'$ are isogonal as are pairs $CB',$ $CA'$ and $BA',$ $BC'.$ Then three lines $AA',$ $BB',$ and $CC'$ are concurrent, i.e., meet at a common point.
| What if applet does not run? |
Napoleon's theorem is obtained when all three angles involved are equal to $30^{\circ}.$ The common point is then known as the First Napoleon point. (The Second Napoleon Point is obtained when the equilateral triangles are formed internally to the given triangle. Similarly, there are two Fermat's points, which are also known as the first and second isogonic centers.) If the base angles are just equal between themselves, the theorem bears the name of Ludwig Kiepert who replaced equilateral triangles with isosceles ones. An interesting specification of the theorem is obtained when the three angles add up to $180^{\circ}.$ But the theorem also admits further generalization.
In Theorem 1, pairs of (isogonal) lines were related to angle bisectors. As is well known from elementary geometry, angle bisectors meet at a single point (incidentally, the incenter of the triangle.)
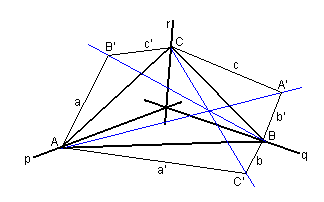
Two lines $AB'$ and $AC'$ through a vertex $A$ of a triangle are said to be isotomic if they intersect the opposite side $BC$ in points equidistant from its midpoint $M_{a}.$ Theorem 1 remains valid for isotomic lines as well. And, in a certain sense, for any three concurrent lines.
A second generalization that I am about to formulate and then prove belongs to the realm of Projective Geometry.
Theorem 2
Let $p, q, r$ be concurrent lines through the vertices $A,$ $B,$ and $C,$ respectively, of $\Delta ABC.$ Let $P_{A}$ be the pencil of lines at $A$ and let $T_{A}$ be the (unique) projective mapping on $P_{A}$ which
- interchanges lines $AB$ and $AC,$
- leaves $p$ fixed.
Define $P_{A},$ $P_{B},$ and $T_{A},$ $T_{B}$ similarly. For any line $a$ in $P_{A},$ let $a'=T_{A}(a).$ Similarly, for $b$ in $P_{B}$ and $c$ in $P_{C},$ let $b'=T_{B}(b)$ and $c'=T_{C}(c).$ Let $C'=a'\cap b,$ $B'=c\cap a,$ and $A'=b'\cap c.$
Then $AA',$ $BB',$ and $CC'$ are concurrent.
Note that (an apparently more general) Theorem 2 follows from Theorem 1 with a projective mapping that leaves vertices $A,B,C$ fixed but takes the incenter into any point $P$ (the intersection of lines $p, q, r.)$
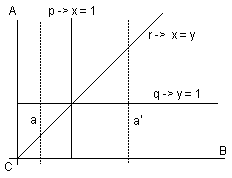
To prove Theorem 2, perform the projective mapping that carries $C$ to the origin, $A$ to the point at infinity at $y$-axis, $B$ to the point at infinity at $x$-axis, and $P$ to the point $(1, 1).$
Lines $p,$ $q,$ and $r$ are carried onto the lines $x = 1,$ $y = 1,$ and $x = y,$ respectively. We thus have
$P_{A}$ is the set of all vertical lines,
$P_{B}$ is the set of all horizontal lines,
$P_{C}$ is the set of all lines through the origin.
Transformation $T_{A}$ preserves the vertical direction and, therefore, is in reality a 1-dimensional projective transformation. So it's a Möbius transformation which, in general, has the form $f(x)=(ax+b)/(cx+d).$ Transformations that interchange $x=0$ with the point at infinity are given by $f(x)=a+b/x$ $(c=1$ and $d=0.)$ Among those, there is a single one that leaves $x=1$ fixed: $f(x)=1/x.$ So $T_{A}$ maps $x=a$ onto $x=1/a.$
To simplify the notations, we will denote the vertical line with $x=a$ by $a,$ the horizontal line $y=b$ by $b,$ and the line $y=cx$ through the origin, by $c.$ Then with similar definitions for $T_{B}$ and $T_{C}$ we have
$a' = T_{A}(a) = 1/a, b' = T_{B}(b) = 1/b,$ and $c' = T_{C}(c).$
Further
$C'=a'\cap b = (1/a, b),$
$B'=c'\cap a = (a, a/c),$ and
$A'=b'\cap c = (1/(bc), 1/b).$
Thus $AA'$ is described by the $x=1/(bc),$ $BB'$ the equation $y=a/c,$ and $CC'$ by the equation $y = (ab)x.$ Then, $AA'\cap BB' = (1/(bc), a/c)$ which lies on the line $CC'.$
Looking back at the two theorems, the fact that Theorem 2 is a theorem of Projective Geometry implies that Theorem 1 belongs to Absolute Geometry. As such, besides Euclid's, it also holds in geometries of Riemann and Lobachevsky. (In the later, existence of points $A',$ $B',$ $C'$ must be stipulated.)
Reference
- R. Courant and H. Robbins, What Is Mathematics?, Oxford University Press, 1996
- H. S. M. Coxeter, Introduction to Geometry, John Wiley & Sons, NY, 1961
- H. S. M. Coxeter and S. L. Greitzer, Geometry Revisited, MAA, 1967
- H. Dorrie, 100 Great Problems Of Elementary Mathematics, Dover Publications, NY, 1965.
- D. Gale, Mathematical Entertainments, The Math Intelligencer, v18, n1, 1996, p31-34 (reprinted in D. Gale, Tracking The Autmatic Ant, Springer-Verlag, 1998)
- F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991, pp. 1175-1177
- R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 1960
- R. Honsberger, Mathematical Gems I, MAA, 1973.
- D. Pedoe, Circles: A Mathematical View, MAA, 1995.
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1970.
- V. M. Tikhomirov, Stories About Maxima and Minima, AMS/MAA, 1990.
- D. Wells, You are a Mathematician, John Wiley & Sons, 1995
E. Torricelli is sometimes said to be a student of Galileo [Honsberger, p. 24], which is not quite correct. Torricelli was not directly a student of Galileo, but rather of Galileo's student Bendetto Castelli. Castelli did introduce Torrecelli's work to Galileo, who then invited Torricelli to come to work with him in Florence. Unfortunately, Torricelli could not come until 1641, and Galileo died in early January, 1642, so their cooperation was rather short. Upon Galileo's death, Torricelli was named the successor of Galileo as the court mathematician to the Grand Duke of Tuscany. He lived and died in the ducal palace in Florence.
Napoleon's Theorem
- Napoleon's Theorem
- A proof with complex numbers
- A second proof with complex numbers
- A third proof with complex numbers
- Napoleon's Theorem, Two Simple Proofs
- Napoleon's Theorem via Inscribed Angles
- A Generalization
- Douglas' Generalization
- Napoleon's Propeller
- Napoleon's Theorem by Plane Tessellation
- Fermat's point
- Kiepert's theorem
- Lean Napoleon's Triangles
- Napoleon's Theorem by Transformation
- Napoleon's Theorem via Two Rotations
- Napoleon on Hinges
- Napoleon on Hinges in GeoGebra
- Napoleon's Relatives
- Napoleon-Barlotti Theorem
- Some Properties of Napoleon's Configuration
- Fermat Points and Concurrent Euler Lines I
- Fermat Points and Concurrent Euler Lines II
- Escher's Theorem
- Circle Chains on Napoleon Triangles
- Napoleon's Theorem by Vectors and Trigonometry
- An Extra Triple of Equilateral Triangles for Napoleon
- Joined Common Chords of Napoleon's Circumcircles
- Napoleon's Hexagon
- Fermat's Hexagon
- Lighthouse at Fermat Points
- Midpoint Reciprocity in Napoleon's Configuration
- Another Equilateral Triangle in Napoleon's Configuration
- Yet Another Analytic Proof of Napoleon's Theorem
- Leo Giugiuc's Proof of Napoleon's Theorem
- Gregoie Nicollier's Proof of Napoleon's Theorem
- Fermat Point Several Times Over
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73574848
