Miguel Ochoa's van Schooten Is a Slanted Viviani

Miguel Ochoa's van Schooten Is a Slanted Viviani:
An Ultimate Generalization

What Might This Be About?

Problem

In $\Delta ABC,$ circle $(O)$ through $A$ and cuts $BC$ in $D_1$ and $D_2$ and sides $AB$ and $AC$ in $E$ and $F,$ respectively.

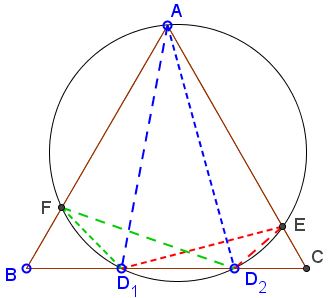
Miguel Ochoa's van Schooten ultimate generalization, problem

Prove that $D_1E + D_1F = AD_2$ and $D_2E + D_2F=AD_1.$

Proof

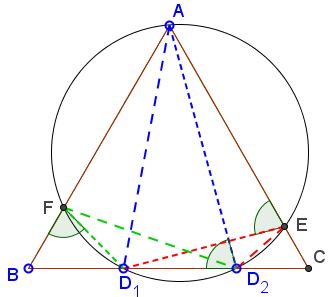
As has been done previously, $\angle D_1FB=\angle AD_2B=\angle D_1EA.$ It thus follows from the slanted Viviani theorem that $D_1E + D_1F = AD_2.$ $D_2E + D_2F=AD_1$ is proved similarly.

Miguel Ochoa's van Schooten ultimate generalization, problem

Acknowledgment

Gobbalipur Jayanth has shown that his previous proof extends to the case where the given circle is not required to be tangent to the base $BC.$ His proof easily handles the more general case. However, as was observed by Grégoire Nicollier, both follow from the slanted Viviani theorem. Above, we have adopted Grégoire's approach.

Related material Read more...

	Angle Trisectors on Circumcircle
	Equilateral Triangles On Sides of a Parallelogram
	Pompeiu's Theorem
	Pairs of Areas in Equilateral Triangle
	The Eutrigon Theorem
	Equilateral Triangle in Equilateral Triangle
	Seven Problems in Equilateral Triangle
	Spiral Similarity Leads to Equilateral Triangle
	Parallelogram and Four Equilateral Triangles
	A Pedal Property in Equilateral Triangle
	Miguel Ochoa's van Schooten Like Theorem
	Two Conditions for a Triangle to Be Equilateral
	Incircle in Equilateral Triangle
	When Is Triangle Equilateral: Marian Dinca's Criterion
	Barycenter of Cevian Triangle
	Excircle in Equilateral Triangle
	Converse Construction in Pompeiu's Theorem
	Wonderful Trigonometry In Equilateral Triangle
	60^o Angle And Importance of Being The Other End of a Diameter
	One More Property of Equilateral Triangles
	Van Khea's Quickie
	Equilateral Triangle from Three Centroids

72520243