Miguel Ochoa's van Schooten Like Theorem II

What Might This Be About?

10 May 2015, Created with GeoGebra

Problem

In $\Delta ABC,$ circle $(O)$ through $A$ and tangent to $BC$ in $D$ cuts $AB$ and $AC$ in $E$ and $F,$ respectively.

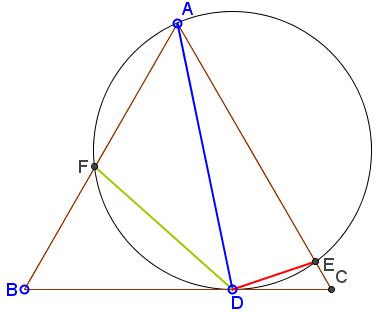
Miguel Ochoa's van Schotten Like Theorem, problem

Prove that $DE = DF + AD.$

In the notations I follow the original formulation:

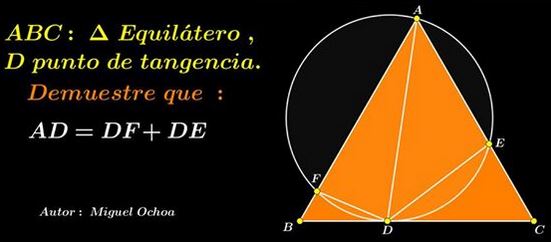
Miguel Ochoa's van Schotten Like Theorem, original problem

Proof 3

Two other proofs can be found on a sister page. It seems to me that the present proof due to its elegance deserves to be treated separately.

Find point $X$ on $(O)$ for which $\Delta EFX$ is equilateral. This is possible because $\angle EAF=60^{\circ}.$ Two configurations are possible; both treated in the same way. Here's one:

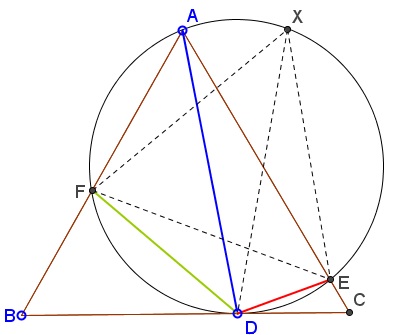
Miguel Ochoa's van Schotten Like Theorem, solution 3

For the secant angle $ABD$ we have (in terms of arcs):

$\displaystyle\begin{align} 60^{\circ}&=\angle ABD\\ &= \frac{1}{2}\left(\widehat{DE}+\widehat{EX}+\widehat{XA}-\widehat{DF}\right)\\ &= \angle DFE + 60^{\circ}+\angle AFX - \angle DEF. \end{align}$

In other words $\angle DEF =\angle DFE+\angle AFX.$ From here,

$\displaystyle\begin{align} \angle AFD &= \angle AFX + \angle EFX + \angle DFE\\ &= \angle AFX + 60^{\circ} + \angle DFE\\ &= \angle DEF + 60^{\circ}\\ &= \angle DEF + \angle FEX\\ &= \angle DEX. \end{align}$

Since equal inscribed angles are subtended by equal chords, $AD=XD.$ But, by van Schooten's theorem, $XD=DE+DF$ so that, too, $AD=DE+DF,$ as required.

Acknowledgment

The above statement has been posted by Miguel Ochoa Sanchez at the CutTheKnotMath facebook page. The proof is by Josué García Piscoya. Another elegant proof by Gobbalipur Jayanth can be found on a separate page.

71873192