Triangle of Maximum Area II
Leo Giugiuc posted an optimization problem at the CutTheKnotMath facebook page together with a solution (Solution 1) by Claudia Nanuti, Diana Trailescu, Dan Sitaru and Leo Giugiuc and with a reference to the Mathematical Inequalities facebook group.
Let $ABC$ be a triangle whose sides $a,b,c$ satisfy
$1\lt a\le 2\le b\le 5\le c\le 6.$
Find maximum possible area of $\Delta ABC.$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyLet $ABC$ be a triangle whose sides $a,b,c$ satisfy
$1\lt a\le 2\lt b\le 5\lt c\le 6.$
Find maximum possible area of $\Delta ABC.$
Solution 1
Let $x=c^2\in (25,36],\;$ $y=b^2\in (9,25],\;$ $z=a^2\in (1,4].$ By Heron's formula, for the area $[\Delta ABC]\;$ of $\Delta ABC\;$ we have
$16[\Delta ABC]^2=-x^2+2(y+z)x-(y-z)^2.$
The function $f(x)=-x^2+2(y+z)x-(y-z)^2\;$ attains its maximum at $x=y+z:\;$ $f(x)\le f(y+z)=4yz,$ implying that $f(x)\le 400.\;$ We observe that that value is attained for $y=25\;$ and $z=4\;$ such that $x=25+4=29.\;$ Thus $\max [\Delta ABC]=5\;$ and is attained with $a=2,\;$ $b=5,\;$ and $c=\sqrt{29}.$
Solution 2
Observe that at least one of $a,b,c$ for which the area of the triangle is maximum ought to be at the upper end of its range, i.e., either $a=2,\;$ or $b=5,\;$ or $c=6.\;$ For, otherwise, it would be possible to expand the triangle (if only a little) by making one of the conditions satisfied without infringing on other constraints.
The three diagrams below illustrate the three possible cases: when one of the sides (viz, the horizontal one) is successively $2,\;$ $5,\;$ and $6.\;$ In each case the area where the remaining constraints are satisfied is filled yellow.
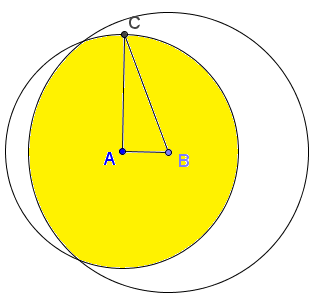
Assume $AB=2.\;$ The yellow area is the intersection of the filled circles $A(5)\;$ and $B(6).\;$ The maximum area is attained for the third vertex $C$ at the top of circle $A(5)\;$ with center $A\;$ and radius $5.\;$ $\Delta ABC\;$ is right with area $\frac{1}{2}2\cdot 5.$

Assume $AB=5.\;$ The yellow area is the intersection of the filled circles $A(2)\;$ and $B(6).\;$ The maximum area is attained for the third vertex $C$ at the top of circle $A(2)\;$ with center $A\;$ and radius $2.\;$ $\Delta ABC\;$ is right with area $\frac{1}{2}2\cdot 5.$
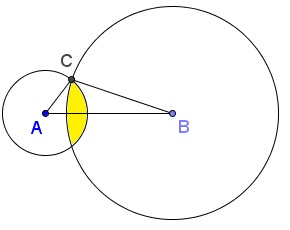
Assume $AB=6.\;$ The maximum area is attained for the third vertex $C$ at the intersection of $A(2)\;$ and $B(5).\;$ In this case, $[\Delta ABC]=\frac{1}{2}2\cdot 5\sin\angle ACB\lt 5.\;$
In the first two cases, by the Pythagorean theorem, $c=\sqrt{29}.$
Proof 3
Grégoire Nicollier has observed that, in general, $[\Delta ABC=\frac{1}{2}ab\sin\angle ACB\;$ is a function that depends linearly on the independent variables $a,\;$ $b,\;$ and $\sin\angle ACB\;$ so that it attains its maximum when each of them takes up the maximum possible value, i.e., in this case, $a=2,\;$ $b=5,\;$ and $\sin\angle ACB=1,\;$ making the maximum area $\frac{1}{2}ab=5.\;$ The only restriction to this happening may come from the hypotenuse $\sqrt{a^2+b^2}\;$ not satisfying the constraint imposed on $c.\;$ But clearly $\sqrt{2^2+5^2}=\sqrt{29}\in (5,6].$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73511657
