2006 Hellenic Mathematical Olympiad, Problem 4
Leo Giugiuc brought to my attention Problem 4 from the 2006 Hellenic Mathematical Olympiad. Solution 1 below is by Dan Sitaru and Leo Giugiuc. Solutions 3, 4, 5 are by Kunihiko Chikaya.
If real numbers $x\;$ and $y\;$ satisfy the condition $x^2 +xy+y^2 = 1,\;$ find the minimum and maximum value of $K = x^3y+xy^3.$
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander BogomolnyIf real numbers $x\;$ and $y\;$ satisfy the condition $x^2 +xy+y^2 = 1,\;$ find the minimum and maximum value of $K = x^3y+xy^3.$
Solution 1
We consider two cases: $xy\ge 0\;$ and $xy\le 0:$
Case 1: $xy\ge 0$
If $x+y=2s\;$ and $xy=p,\;$ then by the AM-GM inequality, $s^2\ge p\;$ and we need to find the extrema of
$xy(x^2+y^2)=xy(1-xy)=p(1-p).$
But $x^2 +xy+y^2 = 1\;$ implies $4s^2-p=1,\;$ i.e., $\displaystyle s^2=\frac{1+p}{4},\;$ such that $\displaystyle\frac{1+p}{4}\ge p,\;$ which gives $\displaystyle p\le\frac{1}{3}.\;$ Since the quadratic $p(1-p)\;$ is strictly increasing on $\displaystyle [0,\frac{1}{3}],\;$ we deduce $\displaystyle 0\le p(1-p)\le\frac{2}{9}.$ $0\;$ is attained at, say, $x=1\;$ and $y=0.\;$ $\displaystyle\frac{2}{9}$ is attained with $\displaystyle x=y=\frac{1}{\sqrt{3}}.$
Case 1: $xy\le 0$
WLOG, let $x\ge 0\ge y.\;$ Set $a=-y\ge 0.\;$ Then $x^2-xa+a^2=1\;$ and we need to find extrema of $-p(1+p),\;$ where $p=xa.\;$ AS before, $4s^2-3p=1,\;$ with $2s=x+y,\;$ implying $\displaystyle s^2=\frac{1+3p}{4}\ge p\;$ so that $p\le 1.\;$ Hence, $-2\le -p(1+p)\le 0.$ $-2\;$ is attained for $x=-y=1.\;$
To sum up: $\min K=-2,\;$ $\max K=\displaystyle\frac{2}{9}.$
Solution 2
Let's make a change of variables: $x=u+v\;$ $y=u-v.;$ Then $x^2+xy+y^2=3u^2+v^2\;$ and $xy(x^2+y^2)=2(u^4-v^4).\;$ The problem is then to find the extrema of $K=2(u^4-v^4),$ subject to $3u^2+v^2=1.$
The latter is an ellipse, while $K=const$ gives two families of hyperbola-like curves:
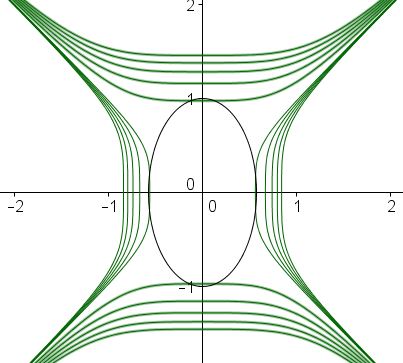
The extrema are achieved by the curves that touch the ellipse. This happens at the vertices of the latter: $(\pm\displaystyle\frac{1}{\sqrt{3}},0)\;$ and $(0,\pm 1).\;$ At these points, the values of $K\;$ are $K(\pm\displaystyle\frac{1}{\sqrt{3}},0)=\frac{2}{9}\;$ and $K(0,\pm 1)=-2.\;$ These are the maximum and the minimum values of $K.\;$
In terms of $x,y,\;$ the maximum is achieved at $x=y=\pm\displaystyle\frac{1}{\sqrt{3}},\;$ the minimum at $x=-y=\pm 1.$
Solution 3
From the constraint $1-xy=x^2+y^2.\;$ Note that $x^2+y^2\ge 2|xy|,\;$ implying $1-xy\ge 2|xy|,\;$ or $\displaystyle -1\le xy\le\frac{1}{3}.\;$
Now, $K=xy(1-xy)\;$ is a quadratic function in $xy\;$ with maximum at $\displaystyle xy=\frac{1}{2}\;$ so that it is monotone on $\displaystyle [-1,\frac{1}{3}].$ From here $\displaystyle -2\le K\le\frac{2}{9}.$ $K=-2\;$ is attained for $x=-y=\pm 1;\;$ $\displaystyle K=\frac{2}{9}\;$ is attained for $\displaystyle x=y=\pm\frac{1}{\sqrt{3}}.$
Solution 4
Note that the constraint $x^2+xy+y^2=1\;$ can be rewritten as $3(x+y)^2+(x-y)^2=4\;$ while $\displaystyle K=\frac{1}{8}\left((x+y)^4-(x-y)^4\right).$ Define $X=(x+y)^2\;$ and $Y=(x-y)^2.\;$
We have $3X+Y=4,\;$ $X,Y\ge 0$ which implies that $\displaystyle 0\le X\le\frac{4}{3}.$ Further,<\p>
$\displaystyle\begin{align} K&=\frac{1}{8}(X^2-Y^2)\\ &=\frac{1}{8}(X^2-(4-3X)^2)\\ &=-(x-1)(x-2). \end{align}$
As a function of $X,\;$ $K\;$ is monotone increasing on $\displaystyle [0,\frac{4}{3}],\;$ etc.
Solution 5
Let $(x,y)=r(\cos\theta ,\sin\theta ).\;$ The constraint becomes $r^2(1+\sin\theta\cos\theta)=1,\;$ or, $\displaystyle\sin\theta\cos\theta =\frac{1-r^2}{r^2}.$ Since $\sin\theta\cos\theta =\frac{1}{2}\sin 2\theta,\;$ $\displaystyle -\frac{1}{2}\le\frac{1-r^2}{r^2}\le\frac{1}{2}.\;$ From here, $\displaystyle\frac{2}{3}\le r^2\le 2.$
Now, $K=xy(x^2+y^2)=r^4\sin\theta\cos\theta=r^2(1-r^2)\;$ which again leads to $\displaystyle -2\le K\le\frac{2}{9}.$
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73581390
