Classification of Quadrilaterals
Quadrilateral is a geometric shape that consists of four points (vertices) sequentially joined by straight line segments (sides). We find the etymology of the word in S. Schwartzman's The Words of Mathematics:
quadrilateral (noun, adjective): the first element is from Latin quadri- "four" from the Indo-European root kwetwer- "four." The second element is from Latin latus, stem later-, "side," of unknown prior origin. A quadrilateral is a four-sided polygon. The Latin term is a partial translation of Greek tetragon, literally "four angles," since a closed figure with four angles also has four sides. Although we use words like pentagon and polygon, the term quadrilateral has completely replaced tetragon.
The seldom used term quadrangle has exactly the same meaning as quadrilateral, however the two related terms -- complete quadrangle and complete quadrilateral -- describe essentially different configurations.
A quadrilateral may be convex or concave (see the diagram below.) A quadrilateral that is concave has an angle exceeding 180o. In either case, the quadrilateral is simple, which means that the four sides of the quadrilateral only meet at the vertices, two at a time. So that two non-adjacent sides do not cross. A quadrilateral that is not simple is also known as self-intersecting to indicate that a pair of his non-adjacent sides intersect.
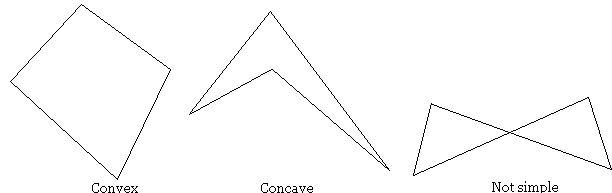
The point of intersection of the sides is not considered a vertex of the quadrilateral.
The shapes of elementary geometry are invariably convex. Starting with the most regular quadrilateral, namely, the square, we shall define other shapes by relaxing its properties.
A square is a quadrilateral with all sides equal and all angles also equal. Angles in any quadrilateral add up to 360°. It follows that, in a square, all angles measure 90°. An equiangular quadrilateral, i.e. the one with all angles equal is a rectangle. All angles of a rectangle equal 90°. An equilateral quadrilateral, i.e. the one with all sides equal, is a rhombus.
In a square, rectangle, or rhombus, the opposite side lines are parallel. A quadrilateral with the opposite side lines parallel is known as a parallelogram. If only one pair of opposite sides is required to be parallel, the shape is a trapezoid. A trapezoid, in which the non-parallel sides are equal in length, is called isosceles. A quadrilateral with two separate pairs of equal adjacent sides is commonly called a kite. However, if the kite is concave, a dart is a more appropriate term. Kite and dart are examples of orthodiagonal quadrilaterals, i.e. quadrilaterals with perpendicular diagonals. A square and a rhombus are also particular cases of this class.
The four vertices of a quadrilateral may be concyclic, i.e., lie on the same circle. In this case, the quadrilateral is known as circumscritptible or, simpler, cyclic. If a quadrilateral admits an incircle that touches all four of its sides (or more generally, side lines), it is known as inscriptible. A quadrilateral, both cyclic and inscriptible, is bicentric.
The diagram below (which is a modification of one from wikipedia.org) summarize the relationship between various kinds of quadrilaterals:
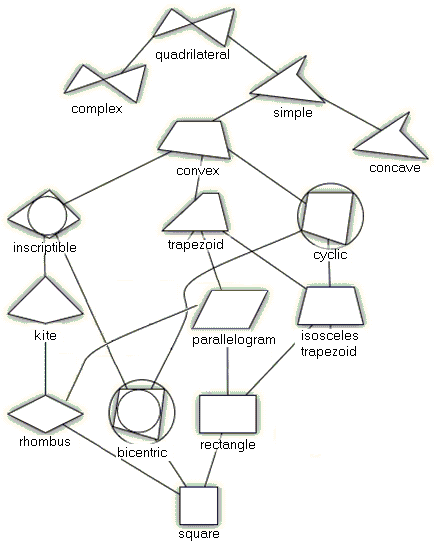
The applet below illustrates the properties of various quadrilaterals. In the applet, one can drag the vertices and the sides of the quadrilateral. You can display its diagonals, angle bisectors and the perpendicular bisectors of its sides. With these props, it's a simple matter to observe every single kind of quadrilateral, with a possible exception of bicentric. Which, too, is not overly difficult if you first get an isosceles trapezoid.)
| What if applet does not run? |
As in the classification of triangles, the definitions may be either inclusive or exclusive. For example, trapezoid may be defined inclusively as a quadrilateral with a pair of parallel opposite sides, or exclusively as a quadrilateral with exactly one such pair. In the former case, parallelogram is a trapezoid, in the latter, it is not. Similarly, a square may or may not be a rectangle or a rhombus. My preference is with the inclusive approach. For, I'd like to think of a square as a rhombus with right angles, or as a rectangle with all four sides equal.
Here is a list of all the properties of quadrilaterals that we have mentioned along with the classes of the quadrilaterals that possess those properties:
| Property | Quadrilaterals | |
| Orthodiagonal | Kite, Dart, Rhombus, Square | |
| Cyclic | Square, Rectangle, Isosceles Trapezoid | |
| Inscriptible | Kite, Dart, Rhombus, Square | |
| Having two parallel sides | Rhombus, Square, Rectangle, Parallelogram, Trapezoid | |
| Having two pairs of parallel sides | Rhombus, Square, Rectangle, Parallelogram | |
| Equilateral | Rhombus, Square | |
| Equiangular | Rectangle, Square |
Orthodiagonal or inscriptible parallelogram is a rhombus; cyclic parallelogram is a rectangle. In particular, a parallelogram with equal diagonals is necessarily a rectangle. And not to forget, every simple quadrilateral tiles the plane.
A simple quadrilateral with two pairs of equal opposite angles is a parallelogram. (Because then the opposite sides are parallel.) A simple quadrilateral with two pairs of equal opposite sides is a parallelogram. (Because of SSS when you draw one of the diagonals.)
There is a simple quadrilateral with two pairs of equal sides: a kite (or a dart). It does have a pair of opposite equal angles.
Nathan Bowler suggested a general construction of a quadrilateral with a pair of equal opposite sides and a pair of equal opposite angles which is not necessarily a parallelogram (there is a dynamic illustration):
Let ABC be isosceles with AB = AC. Pick D on BC. Let C' be the reflection of C in the perpendicular bisector of AD. ABDC' has two opposite sides the same length and two opposite angles equal but is not a parallelogram if D isn't the midpoint of AB. This construction gives all such quadrilaterals.
For an isosceles trapezoid ABCD with AB = CD, the quadrilateral ABDC has a pair of equal opposite sides and two pairs of equal opposite angles.
References
- S. Schwartzman, The Words of Mathematics, MAA, 1994
Related material
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73384789
