A Problem of Hinged Squares
What is it?
A Mathematical Droodle

Discussion

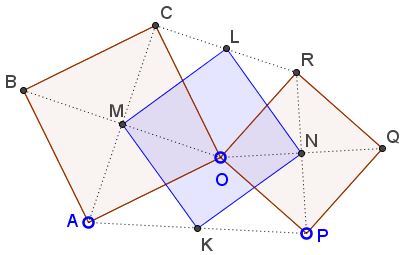
In the applet two squares $OABC$ and $OPQR$ share a common vertex. $M$ and $N$ are centers of the two squares. $K$ and $L$ are the midpoints of $AP$ and $CR,$ respectively. It appears that the quadrilateral $KMLN$ is a square. This is indeed so and is known as the Finsler-Hadwiger theorem.

Consider triangles $AOR$ and $COP.$ $OR = OP.$ Moreover one may be obtained from the other by a suitable rotation through $90^{\circ}$ around $O.$ $OA = OC.$ These too map on each other by the same rotations. Finally, the same is true of triangles $AOR$ and $COP,$ which are thus equal. From here, $AR = CP$ and the two line segments are perpendicular.

In $\Delta APR,$ $KN$ that connects midpoints of sides $AP$ and $PR$ is parallel and equal to half $AR.$ Similarly, in $\Delta ACP,$ $KM$ is parallel and equal to half $CP.$ Therefore, $KM = KN$ and the two are perpendicular.

In an absolutely similar fashion, from the geometry of triangles $CPR$ and $ACR,$ $LM = LN$ and the two are perpendicular. This proves that $KMLN$ is in fact a square.

A Problem of Hinged Squares

Here is another proof. Let $M_{90^{\circ}},$ $N_{90^{\circ}},$ and $K_{180^{\circ}}$ denote the rotations around $M$ through $90^{\circ},$ around $N$ through $90^{\circ},$ and around $K\,$ through $180^{\circ}.$ For example, $M_{90^{\circ}}(A) = O,$ $N_{90^{\circ}}(O) = P,$ $K_{180^{\circ}}(P) = A.$ The composition of the three rotations has a fixed point at $A$ and is a rotation through $360^{\circ} = 0^{\circ}\;(\text{mod}\;360^{\circ}).$ It is therefore a translation with a fixed point, i.e. the identity transformation.

Denote the image of $M$ under $N_{90^{\circ}}$ as $M':$ $M' = N_{90^{\circ}}(M).$ ($\Delta MNM'$ is isosceles with angle $N$ being $90^{\circ}.)\;$ Then

$M = K_{180^{\circ}}(N_{90^{\circ}}(M_{90^{\circ}}(M))) = K_{180^{\circ}}(N_{90^{\circ}}(M)) = K_{180^{\circ}}(M'),$

It follows that $M = K_{180^{\circ}}(M').$ But $K_{180^{\circ}}(M')$ is a reflection in $K.$ Therefore $K$ is the midpoint of $MM'.\;$ Therefore $\Delta MNK$ is isosceles with angle $K$ being $90^{\circ}.$

Remark

Squares $OABC$ and $OPQR$ are constructed on the sides $OA$ and OP of $\Delta AOP.\;$ We have just showed that the center of the square built on the line $MN$ of their centers coincides with the midpoint $K$ of $AP.\;$ This fact is known as Neuberg's Theorem.
The Finsler-Hadwiger theorem is also a special case of the Fundamental Theorem of Directly Similar Figures
The theorem is directly equivalent to one of Thébault's statements.

References

R. L. Finney, Dynamic Proofs of Euclidean Theorems, Math Magazine, 43, pp. 177-185.
R. Honsberger, In Pólya's Footsteps, MAA, 1997

71867148

A Problem of Hinged Squares What is it? A Mathematical Droodle

Discussion

Remark

References

A Problem of Hinged Squares
What is it?
A Mathematical Droodle