Cut The Knot! An interactive column using Java applets by Alex Bogomolny

Napoleon's Propeller

July 2002

As the two most recent columns have been devoted to synthetic proofs of a curious result, I've been looking for an example or two of an illuminating analytic proof. I found quite a few. Two such appear below. In the process I made a small, but surprising, discovery that is reflected in the title of the present column.

Three altitudes of a triangle meet at a point known as the orthocenter of the triangle. There are many proofs of that result. Here's one that uses complex numbers.

Given ΔABC, we may assume its vertices lie on a circle centered at the origin of a Cartesian coordinate system. Let's think of points in the plane as complex numbers. Define H = A + B + C, a simple symmetric function of all the vertices. In fact, H is the common point of the three altitudes of the triangle.

Indeed, for AH and BC to be orthogonal, the ratio (H - A)/(B - C) must be purely imaginary. But

	(H - A)/(B - C)	= (H - A)·(B - C)*/|B - C|2
		= (B + C)·(B - C)*/|B - C|2
		= (|B|2 + B*C - BC* - |C|2)/|B - C|2
		= (B*C - BC*)/|B - C|2

where ^* denotes the conjugate operator. If X denotes the latter expression, X = -X^* and is therefore purely imaginary. So that AH and BC are orthogonal, as expected. Similarly, BH is perpendicular to AC and CH to AB.

The proof admits an elegant shortcut [Hahn, p. 71] that appeals to geometric intuition. Note that

which in particular means that H - A is parallel to the line joining the origin - the circumcenter of ΔABC - with the midpoint of BC, a chord in the circumcircle. In other words, AH is perpendicular to BC, and similarly for BH and CH.

The proof delivers more than was expected. With just a few sentences, not only we get an explicit expression for the orthocenter, the form of the expression (A + B + C) makes it hard to avoid a juxtaposition with the centroid (A + B + C)/3 of the triangle and discovery of the Euler line.

The modified variant is short, powerful and illuminating, at least on a par with several synthetic proofs. Following is an example where the analytic apparatus of complex numbers is used with clarity unmatched by purely geometric proofs I can think of.

Let two triangles be similar and similarly oriented [Wells, p. 20]. Then the midpoints of the segments joining their corresponding vertices form a third triangle similar to the other two.

Two triangles ABC and A'B'C' are similar iff, say, (B - A)/(C - A) = (B' - A')/(C' - A'). The condition means that not only the ratio of lengths of the pairs of sides AB/AC and A'B'/A'C' are equal but that also the angles between them are the same. In the language of determinants the condition for (direct) similarity of two triangles is simply

(1)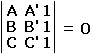

If l = 1/2 and m = 1/2, this is equivalent to

(1')

The assertion is thus immediate as is the generalization for l + m = 1, or in fact, for any l and m not simultaneously 0. (This is a particular case of the Fundamental Theorem of Directly Similar Figures: if the lines connecting the corresponding vertices of two directly similar polygons are devided in equal ratios, then the resulting polygon is directly similar to the given two. Steve Gray has reminded me in a private correspondence that the Fundamental Theorem of Directly Similar Figures, or more specifically (1'), with complex coefficients yields an elegant theorem concerning two triples of similar triangles.)

With (1), it is easy to determine when a triangle is equilateral. The condition is

The latter is equivalent to A² + B² + C² - AB - BC - AC = 0, which is the same as

where j is a rotation through 120° (in the positive direction): j² + j + 1 = 0. Therefore, depending on the orientation of ΔABC, either A + jB + j²C = 0, or A + j²B + jC = 0. The former is the criterion used in Connes' proof of Morley's theorem. [Hahn, p. 60, Pedoe, p. 184]. For a positively oriented triangle, the criterion might have also been obtained more directly from

(2)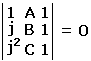

Of course, (2) could be used to derive Napoleon's theorem. The proof is exceptionally clear. Another proof with complex numbers, although straightforward, is longer and might appear somewhat obscure. However, it delivers an easily overlooked surprise.

Let O_C, O_A, and O_B be the centers of the Napoleon triangles erected on the sides of ΔABC. Then easy computations show that

(3)	OAOB = XB + dXC, OBOC = XC + dXA, OCOA = XA + dXB,

where d is the rotation through 60° in the positive direction (d² - d + 1 = 0), X_A = (B + C - 2A)/3, and similarly for X_B and X_C. Since d² = j, Napoleon's theorem now follows from (2) and (3). However, (3) warrants a second look.

X_A equals two thirds of the median in ΔABC (looked at as a complex number) drawn from vertex A, and similarly for X_B and X_C.

(Indeed, (B + C)/2 - A = (B + C - 2A)/2 is the complex number "from A to (B+C)/2," a median of ΔABC. But (B + C - 2A)/3 = 2/3·(B + C - 2A)/2.)

It's clear then that ΔX_AX_BX_C is equal to ΔABC, but has its center at the origin. (Triangles ABC and X_AX_BX_C are not just equal. They are centrally symmetric to each other.) (3), therefore, says something about ΔABC. If ΔX_AX_BX_C is rotated through 60° and its vertices are added pairwise after a cyclic permutation to the vertices of its image, the three complex numbers thus obtained form an equilateral triangle. (To make the picture more compact, we may join the vertices of ΔX_AX_BX_C to those of its rotated image and consider the triangle formed by the midpoints of these segments. The midpoints, too, form an equilateral triangle.)

Here's a surprise. The origin, X_A and dX_A also form an equilateral triangle, and the same holds for the other two triples. The whole picture is exactly that of the Asymmetric Propeller. In the applet below, we may see either two equal triangles at 60° to each other, or the three equilateral triangles formed by the pairs of complex numbers corresponding to the matching vertices of those triangles, or a combination of the above.

Napoleon's theorem is equivalent to the Asymmetric Propeller's theorem! How small is the world! Now, both the original Asymmetric Propeller and Napoleon's theorem start with three equilateral triangles and discover the fourth one by construction. It might have been natural to look for a link between the two results. I never saw the link established by synthetic means.

Martin Gardner wrote about the Asymmetric Propeller in 1999 in a paper that since has been reprinted in his latest collection Gardner's Workout. In the Postscript to the corresponding chapter, Gardner mentions another problem [see also Honsberger, p. 274-276] described to him by Leon Bankoff. (This is in fact the Finsler-Hadwiger Theorem.) That problem admits a simple synthetic solution and, as a consequence of Neuberg's Theorem, another one using complex numbers. It's also a special case of the Fundamental Theorem of Directly Similar Figures.

References

1. M. Gardner, Gardner's Workout, A K Peters, 2001
2. Liang-shin Hahn, Complex Numbers & Geometry, MAA, 1994
3. R. Honsberger, In Pólya's Footsteps, MAA, 1997
4. D. Pedoe, Geometry: A Comprehensive Course, Dover, 1970
5. D. Wells, You Are a Mathematician, John Wiley & Sons, 1997

Napoleon's Theorem

• Napoleon's Theorem
• A proof with complex numbers
• A second proof with complex numbers
• A third proof with complex numbers
• Napoleon's Theorem, Two Simple Proofs
• Napoleon's Theorem via Inscribed Angles
• A Generalization
• Douglas' Generalization
• Napoleon's Propeller
• Napoleon's Theorem by Plane Tessellation
• Fermat's point
• Kiepert's theorem
• Lean Napoleon's Triangles
• Napoleon's Theorem by Transformation
• Napoleon's Theorem via Two Rotations
• Napoleon on Hinges
• Napoleon on Hinges in GeoGebra
• Napoleon's Relatives
• Napoleon-Barlotti Theorem
• Some Properties of Napoleon's Configuration
• Fermat Points and Concurrent Euler Lines I
• Fermat Points and Concurrent Euler Lines II
• Escher's Theorem
• Circle Chains on Napoleon Triangles
• Napoleon's Theorem by Vectors and Trigonometry
• An Extra Triple of Equilateral Triangles for Napoleon
• Joined Common Chords of Napoleon's Circumcircles
• Napoleon's Hexagon
• Fermat's Hexagon
• Lighthouse at Fermat Points
• Midpoint Reciprocity in Napoleon's Configuration
• Another Equilateral Triangle in Napoleon's Configuration
• Yet Another Analytic Proof of Napoleon's Theorem
• Leo Giugiuc's Proof of Napoleon's Theorem
• Gregoie Nicollier's Proof of Napoleon's Theorem
• Fermat Point Several Times Over

Asymmetric Propeller

1. Asymmetric Propeller (An Interactive Gizmo)
2. Asymmetric Propeller: a Generalization
3. A Case of Similarity
4. Napoleon's Propeller
5. Asymmetric Propeller and Napoleon's Theorem
6. Asymmetric Propeller by Plane Tiling
7. The Final Chapter of the Asymmetric Propeller Story
8. Asymmetric Propeller, the XXI Century

|Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny