Kiepert's Theorem: What Is It?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
|Up| |Contact| |Front page| |Contents| |Eye opener| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
| Buy this applet What if applet does not run? |
One of the consequences of Napoleon's Theorem is the existence of Fermat's point. The latter is the point of concurrency of the three lines, each joining a vertex of the given triangle with the farthest vertex of the opposite Napoleon triangle.
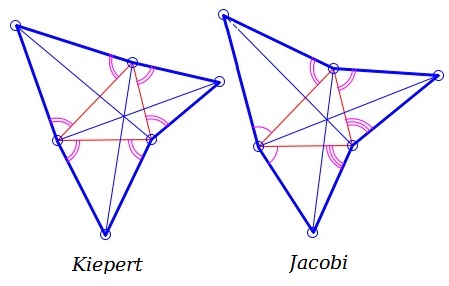
Ludwig Kiepert showed that concurrency takes place when equilateral triangles are replaced with similar isosceles triangles. Kiepert's theorem admits a further generalization where the bases of the isosceles triangles need not coincide with the entire sides of the given triangle.
References
- J. Baker, Napoleon's Theorem and Beyond, Spreadsheets in Education, v. 1, n. 2.
- D. Gale, Tracking The Autmatic Ant, Springer-Verlag, 1998
Napoleon's Theorem
- Napoleon's Theorem
- A proof with complex numbers
- A second proof with complex numbers
- A third proof with complex numbers
- Napoleon's Theorem, Two Simple Proofs
- Napoleon's Theorem via Inscribed Angles
- A Generalization
- Douglas' Generalization
- Napoleon's Propeller
- Napoleon's Theorem by Plane Tessellation
- Fermat point
- Kiepert's theorem
- Lean Napoleon's Triangles
- Napoleon's Theorem by Transformation
- Napoleon's Theorem via Two Rotations
- Napoleon on Hinges
- Napoleon on Hinges in GeoGebra
- Napoleon's Relatives
- Napoleon-Barlotti Theorem
- Some Properties of Napoleon's Configuration
- Fermat Points and Concurrent Euler Lines I
- Fermat Points and Concurrent Euler Lines II
- Escher's Theorem
- Circle Chains on Napoleon Triangles
- Napoleon's Theorem by Vectors and Trigonometry
- An Extra Triple of Equilateral Triangles for Napoleon
- Joined Common Chords of Napoleon's Circumcircles
- Napoleon's Hexagon
- Fermat's Hexagon
- Lighthouse at Fermat Points
- Midpoint Reciprocity in Napoleon's Configuration
|Up| |Contact| |Front page| |Contents| |Eye opener| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
| 49552067 |
