Asymmetric Propeller, the XXI Century
What Is This About?
Introduction
The problem below is a follow-up on the Leo Giugiuc's post at the Romantics of Geometry (Οι Ρομαντικοι της Γεωμετριας) facebook group. His and Dao Thanh Oai's problem has appeared as Problem 4167 in the Crux Mathematicorum.
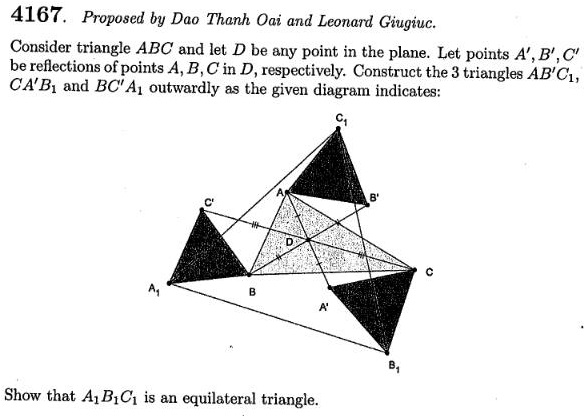
Rather naturally, the problem evoked reminiscence of one of the popular topics of the end of the 20th centuary: the Asymmetric Propeller that was written about by L. Bankoff, P. Erdös, M. Klamkin, M. Gardner, R. Honsberger (see the references elsewhere.)
With time, the Asymmetric Propeller evolved from three equal equilateral triangles to four similar triangles of arbitrary shape. Thus the encounter with the problem 4167 could not but elicit reminiscencies of the earlier problem.
The applet above displays two sets of triangles: red and blue. The existence of the latter for the problem 4167 was pointed out by Antreas Hatzipolakis at the Hyacinthos Yahoo group. For the present problem, the two triangles are equal.
Solution 1 below for the specific case of $\lambda=2\,$ has been supplied by Stathic Koutras. Takis Chronopoulos has kindly translated the original post. That solution does not fully account for all possible positions of point $D\,$ (i.e., for all values of $\lambda.)\,$ Depending on the position of $D\,$ some of the angles change to their supplementary, leaving, however cyclic quadrilaterals as such.
Solution 2 is by Amit Itagi. Amit also noticed that the introduction of arbitray $\lambda\,$ is equivalent to letting point $D\,$ change arbitrarily which it was allowed to do anyway.
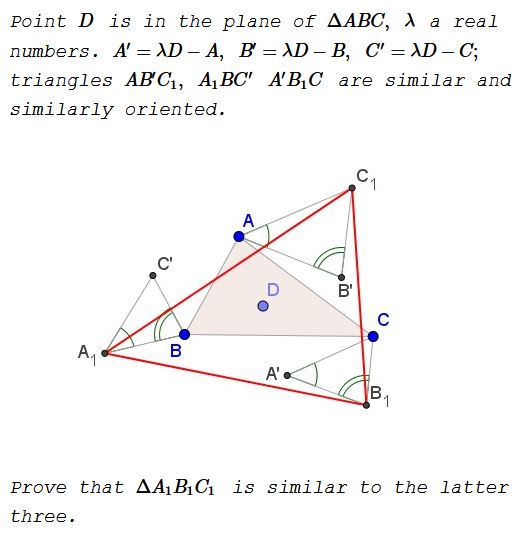
Problem
Solution 1


Solution 2
From the similarity of the three triangles, we can write for some complex number $Z$,
$\displaystyle\begin{align} C'-A_1&=Z(B-A_1) \\ C_1-A&=Z(B'-A) \\ C-A'&=Z(B_1-A'). \end{align}$
Plugging in the $X'=\lambda D - X$ for $X\in\{A,B,C\}$,
$\displaystyle\begin{align} \lambda D - C -A_1&=Z(B-A_1) \\ C_1-A&=Z(\lambda D - B -A) \\ C-\lambda D + A&=Z(B_1-\lambda D + A). \end{align}$
Adding the three equations,
$C_1 - A_1 = Z(B_1-A_1).$
Thus, triangle $A_1B_1C_1$ is similar to the three triangles.
![]()
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73581591
