Napoleon's Theorem by Vectors and Trigonometry
The following proof of Napoleon's theorem is due to Cesare Donolato, Vicenza, Italy.
To remind, Napoleon's theorem asserts that
If equilateral triangles are constructed on the sides of any triangle \(ABC\), then their centers \(N_1\), \(N_2\), \(N_3\) form an equilateral triangle.
Proof
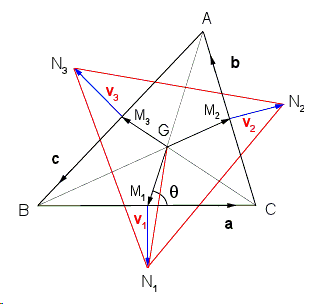
With a reference to the above diagram, the medians \(AM_1\), \(BM_2\), \(CM_3\) of the \(\Delta ABC\) are concurrent at its centroid \(G\), which would also be the center of gravity of three equal point masses placed at the vertices of this triangle. From the definition of center of mass, we have \(\overline{GA} + \overline{GB} + \overline{GC} = \bf{0}\) (overline and bold type designate vectors); by the property of medians, \(\overline{GM_{1}} = - \frac{1}{2}\overline{GA}\), \(\overline{GM_{2}} = - \frac{1}{2}\overline{GB}\), \(\overline{GM_{3}}= - \frac{1}{2}\overline{GC}\), therefore
\( \overline{GM_1} + \overline{GM_2} + \overline{GM_3} = \bf{0}. \)
The vertices \(N_1\), \(N_2\), \(N_3\) of Napoleon's triangle, in agreement with its construction, can be specified in terms of three vectors \(\bf{v}_1\), \(\bf{v}_2\), \(\bf{v}_3\), each of them drawn perpendicularly to a side of \(\Delta ABC\) from its midpoint outward, with \(v_1 = a\sqrt{3}/6\), \(v_2 = b\sqrt{3}/6\), \(v_3 = c\sqrt{3}/6\), where \(v\) denotes the length of vector \(\bf{v}\).
The sides \(a\), \(b\), \(c\) of \(\Delta ABC\) can be represented by the vectors \(\bf{a}\), \(\bf{b}\), \(\bf{c}\) (oriented as shown in the figure) with the obvious property \(\bf{a} + \bf{b} + \bf{c} = \bf{0}\). The \(\bf{v}\) vectors will also have zero sum, because when added up tip-to-tail they form a triangle similar to \(\Delta ABC\) (each \(\bf{v}\) is orthogonal to a side and has magnitude proportional to it):
\( \bf{v}_1 + \bf{v}_2 + \bf{v}_3 = \bf{0}. \)
Since \(\overline{GN_i} = \overline{GM_i} + \bf{v}_i\), (\(i = 1, 2, 3\)), we see that
\( \overline{GN_1} +\overline{GN_2} + \overline{GN_3} = \bf{0}. \)
This equality shows that \(G\) is the center of mass of three equal point masses located at \(N_1\), \(N_2\), \(N_3\), hence \(G\) is also the centroid of Napoleon's triangle. Note that this observation extends to Kiepert's isosceles triangles. The applet below serves a dynamic illustration:
Created with GeoGebra
To prove that the triangle \(N_{1}N_{2}N_3\) is equilateral it is sufficient to show that \(GN_1 = GN_2 = GN_3\); by the law of cosines we have
\(\displaystyle GN_{1}^2 = GM_{1}^2 + v_{1}^2 - 2\cdot GM_1\cdot v_1\cdot \mbox{cos}(\frac{\pi}{2}+\theta). \)
Since \(GM_{1}=\frac{1}{3}AM_{1}\), \(v_{1}=\frac{a\sqrt{3}}{6}\), \(\mbox{cos}(\frac{\pi}{2}+\theta)=-\mbox{sin}(\theta)\),
\(\displaystyle GN_{1}^2 = \frac{1}{9}AM_{1}^2 + \frac{1}{12}a^2 + \frac{2\sqrt{3}}{9}[\frac{1}{2} AM_1\cdot a\cdot \mbox{sin}(\theta)]. \)
The term in square brackets equals the area \(S\) of \(\Delta ABC\), and the median \(AM_1\) of this triangle can be written as a function of its sides as
\(\displaystyle AM_{1}^2 = \frac{2(a^2+b^2+c^2)-3a^2}{4}, \)
implying
\(\displaystyle GN_{1}^2 = \frac{a^2+b^2+c^2}{18} + \frac{2S\sqrt{3}}{9}. \)
This expression is symmetrical in \(a\), \(b\), \(c\), so that it holds for \(GN_2\), \(GN_3\) as well. Therefore, the centroid \(G\) of triangle \(N_{1}N_{2}N_3\) is equidistant from its vertices, i.e., is coincident with the circumcenter; this is a characteristic property of equilateral triangles. The side of the equilateral Napoleon's triangle is \(L = \sqrt{3}\cdot GN_1\), from which we obtain the known expression
\(\displaystyle L^2 = \frac{a^2+b^2+c^2}{6} + \frac{2S\sqrt{3}}{3}. \)
In the more general case of Kiepert's isosceles triangles, the \(\bf{v}\) vectors only change their magnitude to \(v_1 = ka,\) \(v_2 = kb,\) \(v_3 = kc,\) where \(k\) is a proportionality parameter. Thus, by replacing \(v_1\) with \(ka\) in the expression for \(GN_{1}^{2}\) we obtain now
\(\displaystyle GN_{1}^2 = \frac{a^2+b^2+c^2}{18} + \bigg(k^{2}-\frac{1}{12}\bigg)a^{2} + \frac{4kS}{3}. \)
To include the possibility that the \(\mathbf{v}\) vectors point inwards \(\pi/2+\theta\) must then be replaced by \(\pi/2-\theta\); it is sufficient to allow negative values for \(k.\) The above expression becomes symmetrical in \(a, b, c\) for \(\displaystyle k=\pm\frac{\sqrt{3}}{6}:\) the plus sign applies to the outer and the minus to the inner Napoleon's triangle. For the square of the side length we get
\(\displaystyle L^2 = \frac{a^2+b^2+c^2}{6} \pm \frac{2S\sqrt{3}}{3}. \)
Since the area of an equilateral triangle of side \(L\) is \(\displaystyle\frac{\sqrt{3}}{4}L^{2},\) the area of Napoleon triangles is
\(\displaystyle S_{N} = \frac{\sqrt{3}(a^2+b^2+c^2)}{24} \pm \frac{S}{2}. \)
This expression yields the known result that the difference in area of the outer (\(+\)) and inner (\(-\)) Napoleon triangles equals the area \(S\) of the original triangle.
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73608043
