Napoleon on Hinges in GeoGebra
What is this about?
Napoleon's Theorem
Three equilateral triangles $BCD,$ $CAE,$ and $ABF$ are formed outwardly on the sides of $\Delta ABC.$
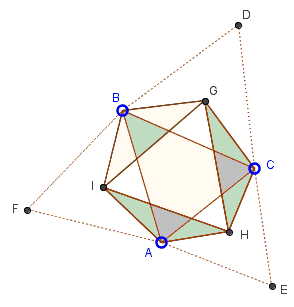
Their respective centroids, $G,$ $H,$ and $I$ form an equilateral triangle.
Hint
There are great many proofs of this popular theorem. The one that the applet above was supposed to suggest is "by a hinged dissection."
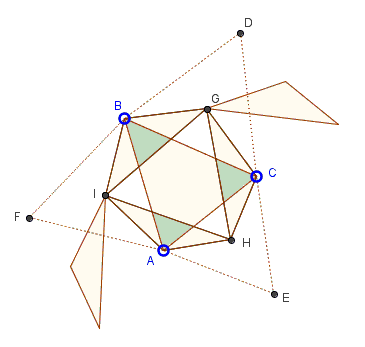
See what happens when, say, triangles $GCH$ and $IAB$ are rotated - one around $G,$ the other around $I$ - until they touch.
Solution
The triangles $GCH$ and $IAB$ when rotated - one around $G,$ the other around $I$ - so $CG$ falls on $BG$ (as they should because $BG=CG,$ by the construction, and $AI$ on $BI,$ for a similar reason, touch along the common side $BH'.$
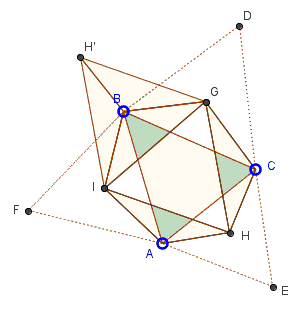
This is because all involved angles are equal $120^{\circ}:$
$\angle BGC = \angle CHA = \angle AIB=120^{\circ}.$
Now consider $\Delta GH'I.$ Its sides are those of $\Delta GHI$ so the two are equal by SSS. Additionally and importantly the angles of $\Delta GH'I$ are all $60^{\circ}.$ For example,
$ \begin{align} \angle IGH' &= \angle IGB+\angle GBH' \\ &= \angle IGB+\angle HGC \\ &= 30^{\circ}+30^{\circ}=60^{\circ}. \end{align} $
It follows that $\Delta GH'I$ is equilateral and, therefore, so is an equal to it triangle $\Delta GHI.$
Acknowledgment
This solution is a reproduction of an older page where the applet was created in Java which is does not run on mobile devices. The present page is - thanks to the GeoGebra software - contains only HTML5 and JavaScript code, both of which are supported by mobile devices.
Napoleon's Theorem
- Napoleon's Theorem
- A proof with complex numbers
- A second proof with complex numbers
- A third proof with complex numbers
- Napoleon's Theorem, Two Simple Proofs
- Napoleon's Theorem via Inscribed Angles
- A Generalization
- Douglas' Generalization
- Napoleon's Propeller
- Napoleon's Theorem by Plane Tessellation
- Fermat's point
- Kiepert's theorem
- Lean Napoleon's Triangles
- Napoleon's Theorem by Transformation
- Napoleon's Theorem via Two Rotations
- Napoleon on Hinges
- Napoleon on Hinges in GeoGebra
- Napoleon's Relatives
- Napoleon-Barlotti Theorem
- Some Properties of Napoleon's Configuration
- Fermat Points and Concurrent Euler Lines I
- Fermat Points and Concurrent Euler Lines II
- Escher's Theorem
- Circle Chains on Napoleon Triangles
- Napoleon's Theorem by Vectors and Trigonometry
- An Extra Triple of Equilateral Triangles for Napoleon
- Joined Common Chords of Napoleon's Circumcircles
- Napoleon's Hexagon
- Fermat's Hexagon
- Lighthouse at Fermat Points
- Midpoint Reciprocity in Napoleon's Configuration
- Another Equilateral Triangle in Napoleon's Configuration
- Yet Another Analytic Proof of Napoleon's Theorem
- Leo Giugiuc's Proof of Napoleon's Theorem
- Gregoie Nicollier's Proof of Napoleon's Theorem
- Fermat Point Several Times Over
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73601897
