Lighthouse at Fermat Points
What is this about?
Problem
Let $ABC$ be a triangle, $F$ is its first (or second) Fermat point. Let $A_1,$ $B_1,$ $C_1$ lie on $BC,$ $CA,$ $AB,$ respectively, such that (using directed angles)
$\angle(\overrightarrow{FA_1},\overrightarrow{FC_1})=\angle(\overrightarrow{FC_1},\overrightarrow{FB_1})=60^\circ$
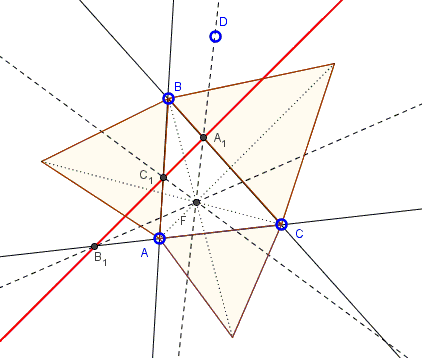
Then $A_1,$ $B_1,$ $C_1$ are collinear.
Hint
The problem reminds of the Lighthouse theorem due to R. K. Guy, but the relation is tenuous. The proof below invokes homothety but does not see to employ Menelaus' theorem.
Solution
The solution draws on the following diagram:

Let $AB'C$ be one of the Napoleon's triangles so that Fermat point $F$ lies on $BB'.$ Let $\Delta IHA_1$ be a homothetic image of $\Delta AB'C,$ with the homothety centered at $B.$ Then $I\in AB,$ $H\in BB',$ $IA_{1}\parallel AC,$ $HA_{1}\parallel B'C,$ $IH\parallel AB',$ and $\Delta IHA_1$ is equilateral.
Let $P$ denote the intersection of $A_1B_1$ with $AB.$ We are going to show that $P=C_1.$
For a start, since $IA_{1}\parallel AB_1,$ triangles $A_{1}IP$ and $B_{1}AP$ are similar, implying
$\displaystyle\frac{A_{1}I}{B_{1}A}=\frac{A_{1}P}{B_{1}P}.$
From $\Delta IHA_1$ being equilateral and $IA_{1}\parallel AB_{1}$ we deduce that
$\angle (\overrightarrow{A_{1}H},\overrightarrow{B_{1}A})=\angle (\overrightarrow{HF},\overrightarrow{AF})=120^\circ,$
and, from here, $\angle FHA_{1}=\angle FAB_1.$ By the construction, $\angle A_{1}FB_{1}=120^\circ$ and, from the property of the Fermat points, $\angle AFB=120^\circ,$ implying $\angle B_{1}FA=\angle A_{1}FH,$ which makes triangles $A_{1}HF$ and $B_{1}AF$ similar:
$\displaystyle\frac{A_{1}H}{B_{1}A}=\frac{FA_{1}}{FB_{1}}.$
Combining the two proportions and bearing in mind that $A_{1}I=A_{1}H,$ we get
$\displaystyle\frac{A_{1}P}{B_{1}P}=\frac{FA_{1}}{FB_{1}}.$
Referring to a property of angle bisectors, this implies that $HP$ is the bisector of $\angle A_{1}FB_{1},$
which exactly means that $P=C_{1},$ as required.
Acknowledgment
This is Theorem 1 from a paper by Dao Thanh Oai announced at the CutTheKnotMath facebook page.
Napoleon's Theorem
- Napoleon's Theorem
- A proof with complex numbers
- A second proof with complex numbers
- A third proof with complex numbers
- Napoleon's Theorem, Two Simple Proofs
- Napoleon's Theorem via Inscribed Angles
- A Generalization
- Douglas' Generalization
- Napoleon's Propeller
- Napoleon's Theorem by Plane Tessellation
- Fermat's point
- Kiepert's theorem
- Lean Napoleon's Triangles
- Napoleon's Theorem by Transformation
- Napoleon's Theorem via Two Rotations
- Napoleon on Hinges
- Napoleon on Hinges in GeoGebra
- Napoleon's Relatives
- Napoleon-Barlotti Theorem
- Some Properties of Napoleon's Configuration
- Fermat Points and Concurrent Euler Lines I
- Fermat Points and Concurrent Euler Lines II
- Escher's Theorem
- Circle Chains on Napoleon Triangles
- Napoleon's Theorem by Vectors and Trigonometry
- An Extra Triple of Equilateral Triangles for Napoleon
- Joined Common Chords of Napoleon's Circumcircles
- Napoleon's Hexagon
- Fermat's Hexagon
- Lighthouse at Fermat Points
- Midpoint Reciprocity in Napoleon's Configuration
- Another Equilateral Triangle in Napoleon's Configuration
- Yet Another Analytic Proof of Napoleon's Theorem
- Leo Giugiuc's Proof of Napoleon's Theorem
- Gregoie Nicollier's Proof of Napoleon's Theorem
- Fermat Point Several Times Over
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73558948
