Fermat's Hexagon

What is this about?

Problem

Let $AA',\;$ $BB',\;$ and $CC'\;$ be three equal line segments lying on concurrent lines at $120^{\circ}$ to each other. Define centroids $G_A,G_B,G_C,K_A,K_B,K_C\;$ of triangles $BCA',\;$ $CAB',\;$ $ABC',\;$ $AB'C',\;$ $A'BC',\;$ $A'B'C,\;$ respectively.

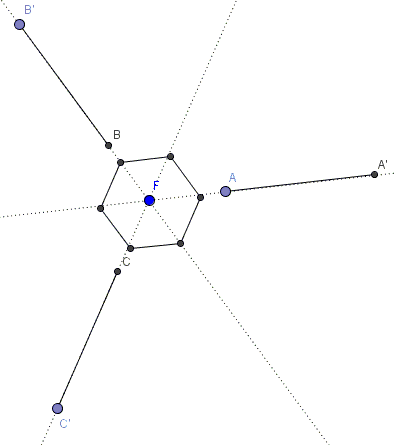
A hexagon in Fermat's segments

The hexagon $G_AK_CG_BK_AG_CK_B$ is regular.

Hint

A look at a related page may prove useful. But so are complex numbers.

Solution

I am going to associate complex numbers with the six given points. Assuming $g$ is the the rotation around the origin through $120^{\circ}$ degrees in the positive direction: $g^3=1,$ and $u,v,w,d$ are fixed real numbers, let's say,

$ \begin{align} A &= u, \\ A' &= u+d, \\ B &= gv, \\ B' &= g(v+d), \\ C &= -gw, \\ C' &= -g(w+d). \end{align} $

Calculating the centroids gives (without the fator $1/3$):

$ \begin{align} G_A &= u+d+gv-gw, \\ G_B &= u+g(v+d)-gw, \\ G_C &= u+gv-g(w+d), \\ K_A &= u+g(v+d)-g(w+d), \\ K_B &= u+d+gv-g(w+d), \\ K_C &= u+d+g(v+d)-gw. \end{align} $

Now it is easy to verify that, say,

$ \begin{align} G_AK_B &= -gd = G_BK_A, \\ G_AK_C &= gd = G_CK_A, \\ G_BK_C &= d = G_CK_B, \end{align} $

which is actually exactly what is needed to establish the assertion.

Acknowledgment

The problem is a generalized reformulation of a post by Dao Thanh Oai at the CutTheKnotMath facebook page.

Napoleon's Theorem

71552581