Fermat Point Several Times Over
A problem involving a special configuration of lines and circles has been posted at the Art of Problem Solving site by Borislav Mirchev with an ingenious analytic solution by Leo Giugiuc.
Problem 1
Through point $B$ inside circle $(O)$ three chords $MQ,$ $NR,$ $PS$ are drawn at $60^{\circ}$ to each other. Six circles are inscribed into the curvilinear triangles so obtained. Let their radii be successively denoted $r_i,$ $i=1,2,\ldots,6.$
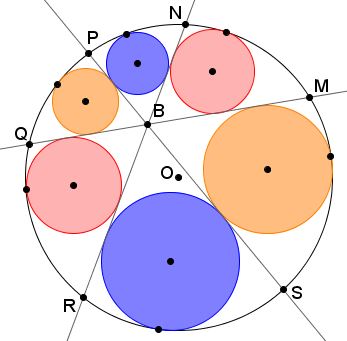
Then $r_{1}r_{3}+r_{3}r_{5}+r_{5}r_{1}=r_{2}r_{4}+r_{4}r_{6}+r_{6}r_{2}.$
Leo subsequently posted the above link at the CutTheKnotMath facebook page which led to conjectures concerning this configuration, some of which became solved problems.
Problem 2
(Posed by Borislav Mirchev; the first solution is by Leo Giugiuc, the second by Stan Fulger)
$BM + BP + BR = BN + BQ + BS.$
Solution 1 to Problem 2
Denote $BM=x,$ $BP=y,$ $BR=z,$ and let $D$ be the intersection of $PR$ and $MQ.$
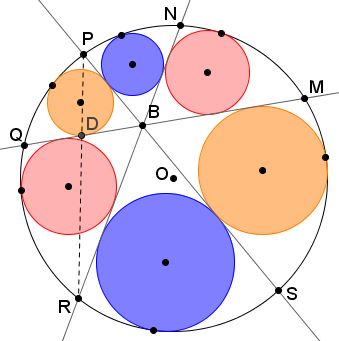
Then $BD$ is the internal angle bisector in $\Delta BPR$ so that $\displaystyle DP=\frac{y\cdot PR}{y+z}$ and $\displaystyle DR=\frac{z\cdot PR}{y+z}.$ In addition, since $\angle PBR=120^{\circ},$ $\displaystyle BD= \frac{yz}{y+z}.$ It follows that
$\displaystyle DM = BD+BM =\frac{yz}{y+z}+x=\frac{xy+yz+zx}{y+z}.$
By the Intersecting Cords Theorem, $DP\cdot DR=DM\cdot DQ$ so that
$\displaystyle DQ=\frac{DP\cdot DR}{DM}=\frac{yz\cdot PR^{2}}{(y+z)^2}\frac{y+z}{xy+yz+zx}=\frac{yz\cdot PR^2}{(y+z)(xy+yz+zx)}.$
Next, in $\Delta PBR,$ the Law of Cosines gives $PR^{2}=y^{2}+yz+z^{2}$ from which $\displaystyle DQ=\frac{yz(y^{2}+yz+z^{2})}{(y+z)(xy+yz+zx)}.$ But $BQ=DQ+DB:$
$\displaystyle BQ=\frac{yz(y^{2}+yz+z^{2})}{(y+z)(xy+yz+zx)}+\frac{yz}{y+z}=yz\frac{(x+y+z)}{xy+yz+zx}.$
Similarly $\displaystyle BS=xz\frac{x+y+z}{xy+yz+zx}$ and $\displaystyle BN=xy\frac{x+y+z}{xy+yz+zx}.$ Adding up and reducing fractions we get
$BN+BQ+BS=x+y+z.$
Solution 2 to Problem 2
Draw circles $(BMR)$ and $(BNQ).$ Line $PS$ bisects the angle at $B$ in triangles $BMR$ and $BNQ,$ implying that it meets the two circles at the mid arcs: one at $A,$ the other at $C.$
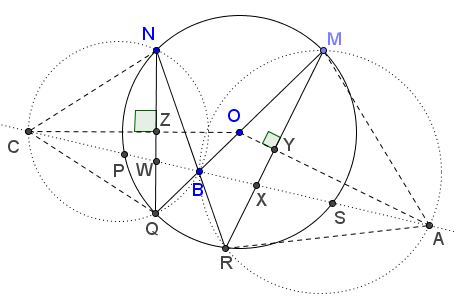
Triangles $AMR$ and $CNQ$ are equilateral such that, by van Schooten's theorem,
$BM+BR=BA\\ BN+BS=BC.$
So in order to prove the required equality $BN+BQ+BS=BM+BP+BR,$ suffice it to show that
$AP=BP+BA = BM+BP+BR\\ CS=BQ+BC = BN+BQ+BS$
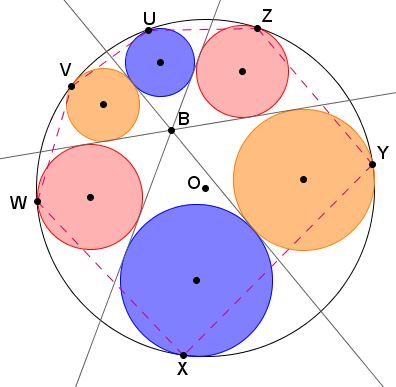
are equal. To this end, join $O$ to $A$ and $C$ and consider the intersections $X,Y,Z,W,$ as in the above diagram. $OA$ is the perpendicular bisector of $MR,$ $OC$ is the perpendicular bisector of $NS.$
$\begin{align} \angle AXM &= \angle ABM + \angle BMR\\ &= \angle ABM + \angle QMR\\ &= \angle CBQ + \angle QNR\\ &= \angle CBN + \angle BNQ\\ &= \angle CWN. \end{align}$
It follows that right triangles $AXY$ and $CWZ$ are similar and $\angle XAY=\angle WCZ,$ i.e., $\angle OAC=\angle OCA,$ making $\Delta AOC$ isosceles. As a consequence, the midpoints of $AC$ and $PS$ coincide, implying $AS=CP,$ and, consequently, $AP=CS,$ as required.
Solution 3 to Problem 2
There is a third solution I placed on a separate page.
Problem 3
(Posed by Daniel Hardisky, with an analitic solution by Leo Giugiuc found elsewhere and synthetic solution below.)
$BM^{2}+BN^{2}+BP^{2}+BQ^{2}+BR^{2}+BS^{2}=6R^{2},$
where $R$ is the radius of $(O).$
Solution 1 to Problem 3
We combine a formula for the area $S\,$ of triangle with sides $a,\,$ $b,\,$ $c,\,$ and circumradius $R:$
$4RS=abc$
with the result of applying the Sine formula for the area for each of the triangles $BMP,\,$ $PBR,\,$ and $MBR:$
$\displaystyle\frac{\sqrt{y^{2}+yz+z^{2}}\sqrt{z^{2}+zx+x^{2}}\sqrt{x^{2}+xy+y^{2}}}{4R}=S=\frac{\sqrt{3}(xy+yz+zx)}{4},$
or,
$\displaystyle 6R^{2}=2\frac{(y^{2}+yz+z^{2})(z^{2}+zx+x^{2})(x^{2}+xy+y^{2})}{(xy+yz+zx)^{2}}.$
Denote $x+y+z=s,\,$ $xy+yz+zx=t,\,$ $xyz=u,\,$ and $BM^{2}+BN^{2}+BP^{2}+BQ^{2}+BR^{2}+BS^{2}=S.\,$ Then, according to what was found in the first solution to the second problem,
$\begin{align} \displaystyle S=S(x,y,z)&=x^{2}+y^{2}+z^{2}+\bigg[(xy)^{2}+(yz)^{2}+(zx)^{2}\bigg]\frac{(x+y+z)^{2}}{(xy+yz+zx)^{2}}\\ &=s^{2}-2t+\frac{s^{2}(t^{2}-2sp)}{t^2}\\ &=2\bigg[s^{2}-t+\frac{s^{3}u}{t^2}\bigg]\\ &=x^{2}+y^{2}+z^{2}+xy+yz+zx-\frac{xyz(x+y+z)^{3}}{(xy+yz+zx)^2}\\ &=(y^{2}+yz+z^{2})+x(x+y+z)\bigg[1-\frac{yz(x+y+z)^{2}}{(xy+yz+zx)^2}\bigg]\\ &=(y^{2}+yz+z^{2})+x(x+y+z)U(x,y,z).\\ \end{align}$
If we introduce $\displaystyle T(x,y,z)=\frac{(y^{2}+yz+z^{2})(z^{2}+zx+x^{2})(x^{2}+xy+y^{2})}{(xy+yz+zx)^{2}},\,$ then what needs to be proved is that $S=T.$
Note that, with $\epsilon =e^{i\frac{2\pi}{3}},$ $y^{2}+y(\epsilon y)+(\epsilon y)^{2}=0$ so that $T(x,y,\epsilon y)=0,$ too. Let's check that the same holds for $S(x,y,\epsilon y).$ Suffice it to check that $U(x,y,\epsilon y)=0:$
Since $1+\epsilon +\epsilon ^{2}=0,\,$ we have
$\begin{align}\displaystyle U(x,y,\epsilon y) &= 1-\frac{\epsilon y^{2}(x+(1+\epsilon )y)^{2}}{(xy+\epsilon y^{2}+\epsilon xy)^{2}}\\ &= 1-\frac{\epsilon y^{2} (x-\epsilon ^{2}y)^{2}}{(-\epsilon ^{2}xy+\epsilon y^{2})^{2}}\\ &= 1-\bigg[\frac{\epsilon^{2}y (x-\epsilon ^{2}y)}{\epsilon^{2}y(-x+\epsilon^{2}y)}\bigg]^{2}\\ &=0. \end{align}$
It follows that both $S(x,y,z)(xy+yz+zx)^2\,$ and $T(x,y,z)(xy+yz+zx)^2\,$ are divisible by $y^{2}+yz+z^{2}.\,$ By analogy, this is also true of the factors $x^{2}+xy+y^{2}\,$ and $z^{2}+zx+x^{2}.\,$ But both $S(x,y,z)(xy+yz+zx)^2\,$ and $T(x,y,z)(xy+yz+zx)^2\,$ are sixth degree polynomials, with coefficients by the sixth degree terms all equal to $1.\,$ Hence, the polynomials are equal and so are $S\,$ and $T.\,$
Solution 2 to Problem 3
Let us consider $B\,$ to be the origin in the complex plane. Let us rotate the circle without loss in generality so that the center of the circle lies on the positive real axis at $O=l+0i.\,$ Note, $l
$\begin{align}&\{r_N\exp[i\phi]-l\} \{r_N\exp[-i\phi]-l\}=R^2\\
&r_N^2-2lr_N\cos\phi-(R^2-l^2)=0 \\
&r_N=l\cos\phi+\sqrt{R^2-l^2\sin^2\phi}.
\end{align}$
We have retained the positive quadratic root. The root with the negative sign for the radical is negative because $R>l.\,$ Following the same procedure for point $R$,
$\begin{align}
r_R&=l\cos(\phi+\pi)+\sqrt{R^2-l^2\sin^2(\phi+\pi)} \\
&=-l\cos\phi+\sqrt{R^2-l^2\sin^2\phi}. \\
r_N^2+r_R^2&=2l^2\cos^2\phi+2(R^2-l^2\sin^2\phi) \\
&=2l^2\cos 2\phi+2R^2.
\end{align}$
Adding similar terms from the other two combinations - $\{P,S\}\,$ and $\{Q,M\},$
$\begin{align}&(r_N^2+r_R^2)+(r_P^2+r_S^2)+(r_Q^2+r_M^2) \\
&=6R^2+2l^2\left[\cos 2\phi + \cos \left(2\phi+\frac{2\pi}{3}\right)
+ \cos \left(2\phi+\frac{4\pi}{3}\right) \right] \\
&=6R^2+2l^2\left[\cos 2\phi + \cos \left(2\phi+\frac{2\pi}{3}\right)
+ \cos \left(2\phi-\frac{2\pi}{3}\right) \right] \\
&=6R^2+2l^2\left[\cos 2\phi + 2\cos 2\phi
\cos\left(\frac{2\pi}{3}\right)\right] \\
&=6R^2+2l^2\cos 2\phi [1+2(-0.5)] \\
&=6R^2\,(QED).
\end{align}$
(Additional (and much simpler) solution is available elsewhere.) The six circle centers lie on a conic.
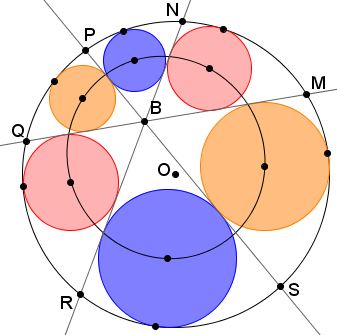
(Posed by Miguel Ochoa Sanchez.) Let $U,$ $V,$ $W,$ $X,$ $Y,$ $Z$ be the points of tangency of the inscribed circles with $(O).$
Then $UV + WX+YZ=VW+XY+ZU.$ (Borislav Mirchev credits this problem to Julio Orihuela, solution is by Leo Giugiuc)
If $O_1,\cdots,O_6$ are the centers of the inscribed circles, then triangles $O_{1}O_{3}O_{5}$ and $O_{2}O_{4}O_{6}$ have equal areas.
It was shown in the solution to Problem 1 that the inscribed circles have the property that their centers are at the distance from $B$ which is twice their radii. Then, if the centers are denoted $O_{i},$ $i=1,\ldots,6$ and the radii $r_{i},$ $i=1,\ldots,6,$ then the Sine formula for the area shows that
$\begin{align}
Area(O_{1}O_{3}O_{5})&= Area(BO_{1}O_{3})+Area(BO_{3}O_{5})+Area(BO_{5}O_{1})\\
&= \frac{\sqrt{3}}{4}(2r_{1}\cdot 2r_{3}+2r_{3}\cdot 2r_{5}+2r_{5}\cdot 2r_{1})\\
&=\sqrt{3}(r_{1}\cdot r_{3}+r_{3}\cdot r_{5}+r_{5}\cdot r_{1})\\
&=\sqrt{3}(r_{2}\cdot r_{4}+r_{4}\cdot r_{6}+r_{6}\cdot r_{2})\\
&=\ldots\\
&= Area(BO_{2}O_{4})+Area(BO_{4}O_{6})+Area(BO_{6}O_{2})\\
&=Area(O_{2}O_{4}O_{6}).
\end{align}$
Point $B$ here is the (first) Fermat point of triangles $MPR$, $NQS,$ and of the two triangles formed by the centers of the inscribed circles. It would not be unexpected if the configuration had additional properties.
|Contact|
|Front page|
|Contents|
|Geometry|
Problem 4
Problem 5
Problem 6
Solution to Problem 6
Remark
![]()
Napoleon's Theorem
73573674
