Circle Chains on Napoleon Triangles
What is this about?
A Mathematical Droodle
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
The applet attempts to suggest a problem by Hirotaka Ebisui:
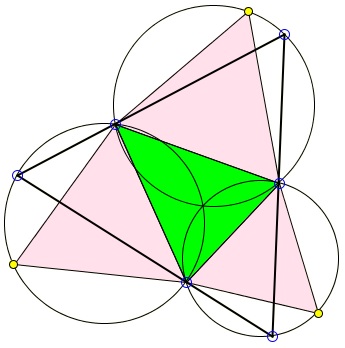
Form equilateral triangles ABC', AB'C, A'BC on the sides of ΔABC and add their circumcircles. Choose point on one of the circumcricles, say D on circle ABC'. Extend DA to its second intersection with circle AB'C in F. Extend FC to its second intersection with circle A'BC in E. Extend EB to its second intersection with circle ABC'. Prove that
- the latter coincides with D, and that
- ΔDEF is equilateral.
| Buy this applet What if applet does not run? |
The problem admits a simple solution based on a combination of two well-known statements. However, I believe that the combination is rather novel; Hirotaka Ebisui deserves full credit for perceiving something new amid a heap of overused theorems.
The circumcricles of Napoleon's triangles are concurrent; in an acute triangle they meet at Fermat's point.
Concurrent circles offer a porism: starting with a point on one and subsequently passing through thepoints of intersections one gets back to the point of departure.
Angles ADB and AC'B are inscribed in the same circle and are subtended by the same arc. They are either equal or supplementary, meaning that ∠ADB is either 60° or 120°. The same holds for the angles at E and F. In both cases ΔEDF is equilateral.
Napoleon's Theorem
- Napoleon's Theorem
- A proof with complex numbers
- A second proof with complex numbers
- A third proof with complex numbers
- Napoleon's Theorem, Two Simple Proofs
- Napoleon's Theorem via Inscribed Angles
- A Generalization
- Douglas' Generalization
- Napoleon's Propeller
- Napoleon's Theorem by Plane Tessellation
- Fermat point
- Kiepert's theorem
- Lean Napoleon's Triangles
- Napoleon's Theorem by Transformation
- Napoleon's Theorem via Two Rotations
- Napoleon on Hinges
- Napoleon on Hinges in GeoGebra
- Napoleon's Relatives
- Napoleon-Barlotti Theorem
- Some Properties of Napoleon's Configuration
- Fermat Points and Concurrent Euler Lines I
- Fermat Points and Concurrent Euler Lines II
- Escher's Theorem
- Circle Chains on Napoleon Triangles
- Napoleon's Theorem by Vectors and Trigonometry
- An Extra Triple of Equilateral Triangles for Napoleon
- Joined Common Chords of Napoleon's Circumcircles
- Napoleon's Hexagon
- Fermat's Hexagon
- Lighthouse at Fermat Points
- Midpoint Reciprocity in Napoleon's Configuration
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2015 Alexander Bogomolny
| 49552156 |
