Two Triples of Similar Triangles
What is this about?
A Mathematical Droodle
What if applet does not run?
-->
21 December 2016, Created with GeoGebra
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
![]()
Draw two triangles, say, A1B1C1 and A2B2C2 both similar (and similarly oriented) to triangle ABC. Choose another triangle, say, 123, and construct three triangles A1A2A3, B1B2B3 and C1C2C3 similar (and similarly oriented) to 123 on the segments A1A2, B1B2 and C1C2, respectively. Then ΔA3B3C3 will be similar to ΔABC!
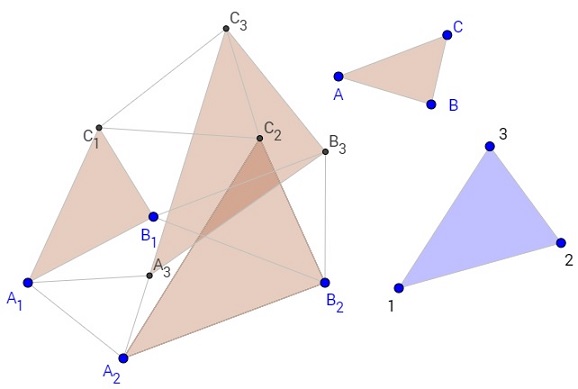
The configuration is completely symmetric between names and indices. One can start with two triangles similar to 123 and after joining their corresponding vertices erect triangles similar to ABC. The newly constructed vertices form then a triangle similar to triangle 123.
If triangles A1B1C1 and A2B2C2 are translations of each other, the result is immediate, and the third triangle A3B3C3 is obtained by translation from either of the first two.
Otherwise, there exists a unique spiral similarity with center O that transforms A1B1C1 into A2B2C2. We then have
It follows that triangles A1OA2, B1OB2 and C1OC2 are similar. But we also assumed the similarity of triangles A1A2A3, B1B2B3 and C1C2C3. So that triangles A1OA3, B1OB3 and C1OC3 are similar, from where
Therefore, ΔA1B1C1 is mapped on ΔA3B3C3 by spiral symmetry. They are, therefore, similar.
Remark
The result we just proved is a formal consequence of the Fundamental Theorem of Directly Similar Figures, in which real coefficients are replaced with complex numbers. (I am grateful to Steve Gray for bringing this to my attention.)
Reference
- H.S.M. Coxeter, S.L. Greitzer, Geometry Revisited, MAA, 1967
- D. Wells, You Are a Mathematician, Dover, 1970
- I. M. Yaglom, Geometric Transformations II, MAA, 1968
![]()
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73579811
