An Extra Triple of Equilateral Triangles for Napoleon
What is this about?
Equilateral Triangles in Napoleon's Configuration
Let $ABC',$ $BCA',$ and $CAB'$ be Napoleon's triangles constructed on the sides of $\Delta ABC.$ Define $A_B$ and $A_C$ as the intersections of $A'B$ and, respectively, $A'C$ with the circumcircle $C(ABC)$ of $\Delta ABC.$ Define similarly $B_A,B_C,C_A,C_B.$
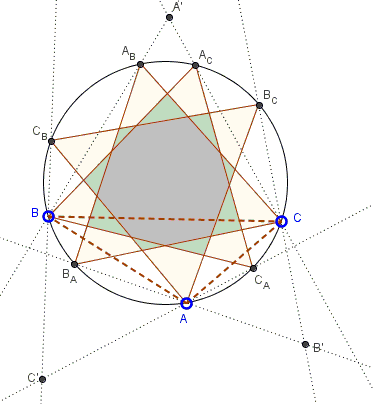
The triangles $A_{B}B_{A}C,$ $AB_{C}C_{B},$ and $A_{C}BC_{A}$ are equilateral.
Hint
The problem is very simple; it submits to chasing inscribed angles.
Solution
Consider, for example, $\Delta AB_{C}C_{B}$ and, more specifically, its side $AB_{C}.$ This is a chord in $C(ABC).$
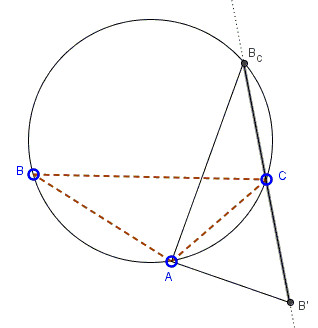
Since $\Delta CAB'$ is equilateral $\angle ACB_C=120^{\circ},$ meaning that side $AB_{C}$ subtends one third of the circumcircle. The same holds for the other sides and for the remaining two triangles.
Acknowledgment
This problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.
Napoleon's Theorem
- Napoleon's Theorem
- A proof with complex numbers
- A second proof with complex numbers
- A third proof with complex numbers
- Napoleon's Theorem, Two Simple Proofs
- Napoleon's Theorem via Inscribed Angles
- A Generalization
- Douglas' Generalization
- Napoleon's Propeller
- Napoleon's Theorem by Plane Tessellation
- Fermat's point
- Kiepert's theorem
- Lean Napoleon's Triangles
- Napoleon's Theorem by Transformation
- Napoleon's Theorem via Two Rotations
- Napoleon on Hinges
- Napoleon on Hinges in GeoGebra
- Napoleon's Relatives
- Napoleon-Barlotti Theorem
- Some Properties of Napoleon's Configuration
- Fermat Points and Concurrent Euler Lines I
- Fermat Points and Concurrent Euler Lines II
- Escher's Theorem
- Circle Chains on Napoleon Triangles
- Napoleon's Theorem by Vectors and Trigonometry
- An Extra Triple of Equilateral Triangles for Napoleon
- Joined Common Chords of Napoleon's Circumcircles
- Napoleon's Hexagon
- Fermat's Hexagon
- Lighthouse at Fermat Points
- Midpoint Reciprocity in Napoleon's Configuration
- Another Equilateral Triangle in Napoleon's Configuration
- Yet Another Analytic Proof of Napoleon's Theorem
- Leo Giugiuc's Proof of Napoleon's Theorem
- Gregoie Nicollier's Proof of Napoleon's Theorem
- Fermat Point Several Times Over
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73615319
