Three Concurrent Chords at 60 Degrees Angles
What Is That About?
A Mathematical Droodle
Created with GeoGebra, 28 November, 2016
Problem
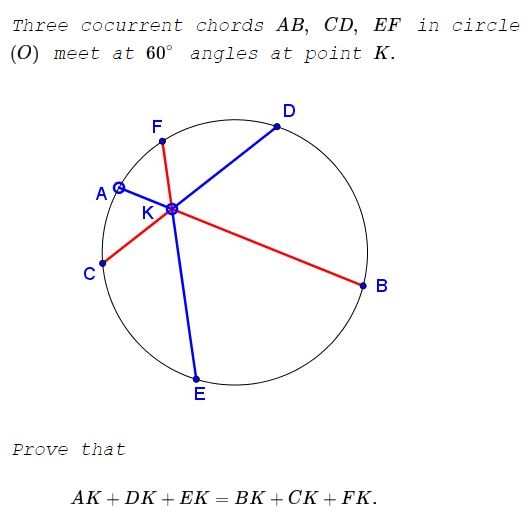
Proof 1
For simplicity, I shall denote $AK=a, BK=b,\ldots,BF=f.\;$ The perpendiculars $OL,\,$ $OM,\,$ $ON\,$ from center $O\,$ of the circle to the chords meet the chords at their midpoints $L,\,$ $M,\,$ $N,\,$ respectively. Thus the circle through those midpoints has $OK\,$ as a diameter.
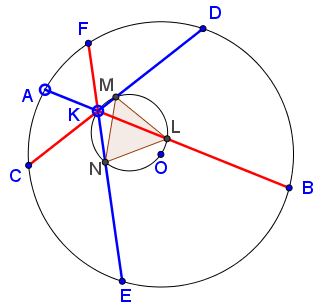
Triangle $LMN\,$ is equilateral as all its angles are $60^{\circ}.\,$ For example, $\angle LMN=\angle LKN (= 60^{\circ})$ as two inscribed angles subtended by the same chord. Let $n\,$ denotes the common side length in $\Delta LMN.$
By the Law of Cosines in $\Delta LMK,$
$\begin{align} n^2&=KL^2+KM^2-2\cdot KL\cdot KM\cos 60^{\circ}\\ &=KL^2+KM^2-KL\cdot KM. \end{align}$
Now, $KL=BK-BL=b-\displaystyle\frac{a+b}{2}=\displaystyle\frac{b-a}{2}.\,$ Similarly, $KM=\displaystyle\frac{d-c}{2},\,$ making
$4n^2=(b-a)^2+(d-c)2-(b-a)(d-c).$
In the same manner, from $\Delta MKN\,$ (now with angle at $K\,$ measuring $12-^{\circ})\,$ we get
$4n^2=(d-c)^2+(e-f)2-(d-c)(e-f).$
Comparing the two right-hand sides gives $(b-a)^2-(b-a)(d-c)=(e-f)^2+(d-c)(e-f),\,$ which can be rewritten as
$(b-a)(b-a-d+c)=(e-f)(e-f+d-c),$
or,
$\displaystyle \frac{b-a}{e-f}=frac{e-f+d-c}{b-a-d+c}.$
Adding now $1\,$ to both side we obtain,
$\displaystyle \frac{b-a+e-f}{e-f}=frac{e-f+b-a}{b-a-d+c}$
where the two fractions have equal numerators and, since they are equal, also equal denominators: $e-f=b-a-d+c,\,$ i.e., $a+d+f=b+c+e.$
Proof 2
We'll change notations a little:
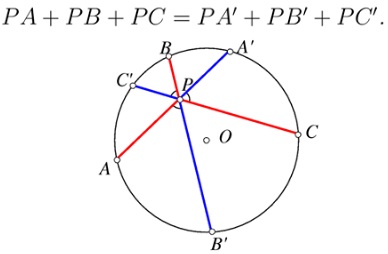
Draw the lines $L_a,L_b,L_c$ perpendicular to $AA',BB',CC'$ at $A,B,C,$ respectively, and the lines $L'_a,L'_b,L'_c$ perpendicular to $AA',BB',CC'$ at $A',B',C',$ respectively. Obviously the equilateral triangles $ABC$ and $A'B'C'$ have pairwise parallel sides and are, therefore homothetic With the center $O.$
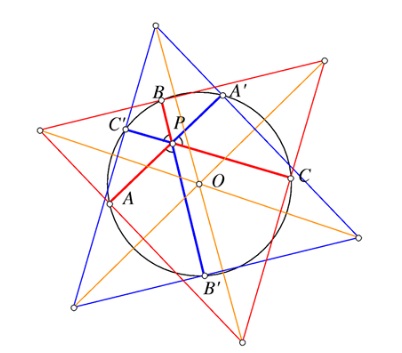
Moreover, since the lines $L'_a,L'_b,L'_c$ are the reflections of $L_a,L_b,L_c,$ the coefficient of homothety is $-1,$ making the two triangles congruent. The sums $PA+PB+PC$ and $PA'+PB'+PC'$ are, due to Viviani's theorem, equal the altitudes in the respective triangles and, therefore, are equal.
Acknowledgment
I am deeply indebted to Rachid El Moussaoui for drawing my attention to this problem and pointing to R. Honsberger's book In the Pólya's Footsteps, where it appears on pp 118-120 with the solution above. Amazingly, I have a bookmark on p 118 of the book and, likely intended to put up a page at the site, but, with time, forgot about it.
Sometimes later I was informed by to Francisco Javier García Capitán about his contacts with Rachid El Moussaoui. It appears that Rachid came across the problem in an online forum where a solution was presented that employed the Viviani theorem. Rachid did not remember the proof but having such a hint led Fransisco Javier to a very elegant solution (Proof 2.)
The problem has been offered at the 15th (1989) All-Russian Mathematical Olympiad for grade 10 - at the time the last high school grade.
P.S. You must love social networks. In a comment to the post at facebook, Leo Giugiuc set things straight for me. I appear that the problem has been discussed elsewhere (Problem 2 there) in 2014, where two additional solutions can be found.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581561
