The Law of Cosines - Another PWW
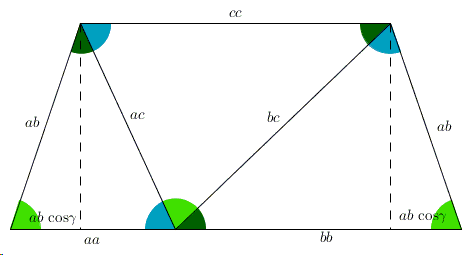
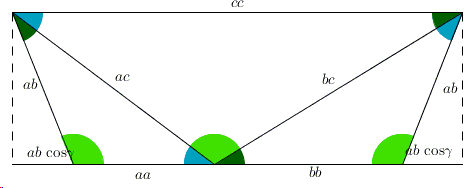
The applet below illustrates a proof without words of the Law of Cosines that establishes a relationship between the angles and the side lengths of \(\Delta ABC\):
\(c^{2} = a^{2} + b^{2} - 2ab\cdot \mbox{cos}\gamma,\)
where \(\gamma\) is the angle in \(\Delta ABC\) opposite side \(c\).
There are four draggable points: the three vertices of the reference triangle and one on the resulting trapezoid.
Proof
The applet illustrates the cases of acute and abtuse triangles, making it it clear that in irder to obtain \(c^2\), for acute triangles, \(2ab\space\mbox{cos}\gamma\) needs to be subtracted from \(a^{2}+b^{2}\), while for obtuse triangles it needs to be added.
(There are several theorems that are proved by similar technique.)
- The Law of Cosines (Cosine Rule)
- The Illustrated Law of Cosines
- The Law of Sines and Cosines
- The Law of Cosines: Plane Tessellation
- The Law of Cosines: after Thâbit ibn Qurra
- The Law of Cosines: Unfolded Version
- The Law of Cosines (Independent of the Pythagorean Theorem)
- The Cosine Law by Similarity
- The Law of Cosines by Larry Hoehn
- The Law of Cosines - Another PWW
- The Law of Cosines - Yet Another PWW
- Law of Cosines by Ancient Sliding
- The Cosine Law: PWW by S. Kung
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73574308
