Concurrent Chords in a Circle, Equally Inclined
What Might This Be About?
Problem
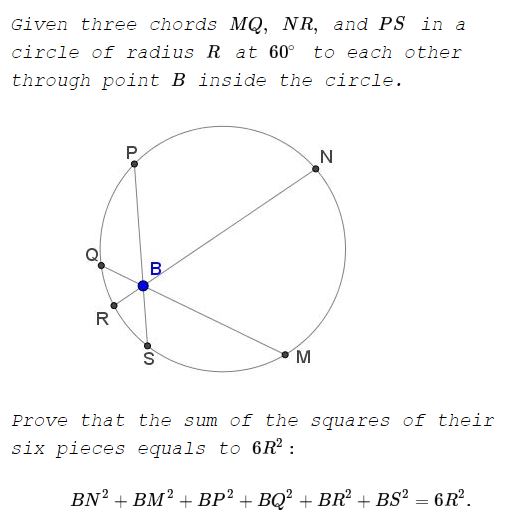
Solution
Vladimir Dubrovsky
30 March, 2017
We'll make use of the Lagrange formula for the moment of inertia, also known as Steiner's and Huygens-Steiner theorem:
For unit masses placed at points $A_1,A_2,\ldots,A_n,\,$ the moment of inertia with respect to a point $X\,$ is defined as $\displaystyle I_X=\sum_{k=1}^nXA_k^2,\,$ and the Lagrange formula takes the form $\displaystyle I_X=nXG^2+I_G,\,$ where $G\,$ is the centroid (center of mass) of these material points.
In particular, $I_X,\,$ as a function of $X,\,$ depends only on the distance $XG.$
The centroid of the six endpoints of the given chords coincides with the centroid of the midpoints of the chords, which are the projections of $O\,$ - the center of the given circle - on the chords, and hence form a triangle inscribed in the circle $\mathbb{c}\,$ with diameter $BO.\,$ By the Inscribed Angle Theorem, the triangle is equilateral.
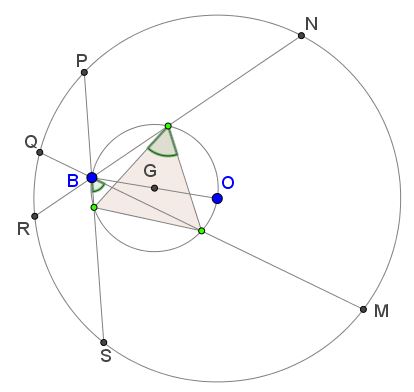
Therefore, its centroid $G\,$ is the center of circle $\mathbb{c},\,$ or the midpoint of $BO.\,$ It follows that $BG=GO,\,$ so, by the Lagrange formula,
$\displaystyle BN^2+BM^2+BP^2+BQ^2+BR^2+BS^2=I_B=I_G=6R^2$
and we are done.
This proof readily generalizes to $n\ge 3\,$ chords drawn through the same point at equal angles to each other: the sum of the squares of their pieces is equal to $nR^2.$
Acknowledgment
The problem has been discussed elsewhere as one of the properties (viz., #3) of the configuration of six concurrent chords. Vladimir Dubrovsky has commented with his solution, reproduced above.
Barycenter and Barycentric Coordinates
- 3D Quadrilateral - a Coffin Problem
- Barycentric Coordinates
- Barycentric Coordinates: a Tool
- Barycentric Coordinates and Geometric Probability
- Ceva's Theorem
- Determinants, Area, and Barycentric Coordinates
- Maxwell Theorem via the Center of Gravity
- Bimedians in a Quadrilateral
- Simultaneous Generalization of the Theorems of Ceva and Menelaus
- Three glasses puzzle
- Van Obel Theorem and Barycentric Coordinates
- 1961 IMO, Problem 4. An exercise in barycentric coordinates
- Centroids in Polygon
- Center of Gravity and Motion of Material Points
- Isotomic Reciprocity
- An Affine Property of Barycenter
- Problem in Direct Similarity
- Circles in Barycentric Coordinates
- Barycenter of Cevian Triangle
- Concurrent Chords in a Circle, Equally Inclined
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73569866
