Surprising 60° in Equilateral Triangle
What Might This Be About?
Source
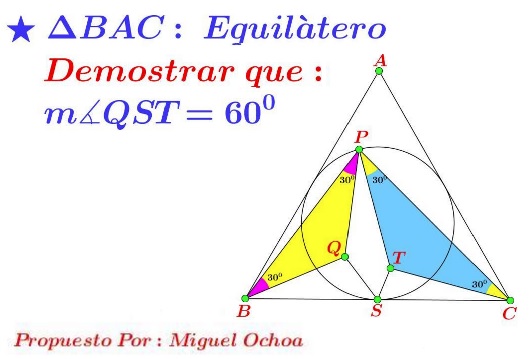
Problem
Let $P\;$ be a point in the upper third of the incircle of an equilateral $\Delta ABC.\;$ Triangles $BPQ\;$ and $CPT\;$ are isosceles with base angles equal $30^{\circ},\;$ as shown.
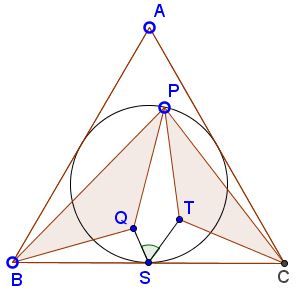
Prove that $\angle QGT=60^{\circ},\;$ where $S\;$ is the midpoint of the base $BC.$
Solution
We shall use complex numbers.
Let $S\;$ be the origin and $x^2+(y-1)^2=1\;$ the equation of the incircle. Then $A=3i,\;$ $C=-B=\sqrt{3},\;$ $P=\cos t+(1+\sin t)i.\;$ Further, $\displaystyle\frac{B-Q}{P-Q}=-\frac{1}{2}+i\frac{\sqrt{3}}{2}.\;$ From here
$\displaystyle\begin{align} Q &= \frac{-2+\sqrt{3}\cos t+\sin t+(\sqrt{3}\sin t-\cos t)i}{2\sqrt{3}}\\ &=\frac{\displaystyle -1+\cos (t-\frac{\pi}{6})+\sin (t-\frac{\pi}{6})i}{\sqrt{3}} \end{align}$
Similarly, $\displaystyle\frac{C-T}{P-T}=-\frac{1}{2}-i\frac{\sqrt{3}}{2},$ implying
$\displaystyle T=\frac{\displaystyle 1+\cos (t+\frac{\pi}{6})+\sin (t+\frac{\pi}{6})i}{\sqrt{3}}.$
To find $\angle QST\;$ we need to calculate $\displaystyle\frac{Q-S}{T-S}.\;$ To this end observe that, for real $x,y,\;$
$\displaystyle\begin{align} -1+\cos x+i\sin x&= 2i\sin\frac{x}{2}\left(\cos\frac{x}{2}+i\sin\frac{x}{2}\right)\\ &= 2\sin\frac{x}{2}\left(\cos\frac{\pi+x}{2}+i\sin\frac{\pi+x}{2}\right),\\ 1+\cos y+i\sin y&=2\cos\frac{y}{2}\left(\cos\frac{y}{2}+i\sin\frac{y}{2}\right). \end{align}$
Taking $\displaystyle x=t-\frac{\pi}{6}\;$ and $\displaystyle y=t+\frac{\pi}{6}\;$ we get
$\displaystyle\begin{align} \frac{Q-S}{T-S}&= \frac{\displaystyle\sin\frac{x}{2}}{\displaystyle\cos\frac{y}{2}}\cdot\frac{\displaystyle\cos\frac{\pi+x}{2}+i\sin\frac{\pi+x}{2}}{\displaystyle\cos\frac{y}{2}+i\sin\frac{y}{2}}\\ &=\frac{\displaystyle\sin\frac{x}{2}}{\displaystyle\cos\frac{y}{2}}\cdot\left(\cos\frac{\pi+x-y}{2}+i\sin\frac{\pi+x-y}{2}\right)\\ &=\frac{\displaystyle\sin\frac{x}{2}}{\displaystyle\cos\frac{y}{2}}\cdot\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right), \end{align}$
implying that $\displaystyle\angle QST=\frac{\pi}{3}.$
Extra
Following the procedure above we can obtain that also $\displaystyle\angle QOT=\frac{\pi}{3},\;$ where $O\;$ is the center of $\Delta ABC.\;$ This shows that the circles $(QGT)\;$ and $(QOT)\;$ are equal. In addition, as it follows from the expression for $Q\;$ and $T\;$ obtained above, $Q\;$ lies on the circle $\displaystyle (x+\frac{\sqrt{3}}{3})^2+y^2=\frac{1}{3}\;$ while $T\;$ lies on the circle $\displaystyle (x-\frac{\sqrt{3}}{3})^2+y^2=\frac{1}{3}.$
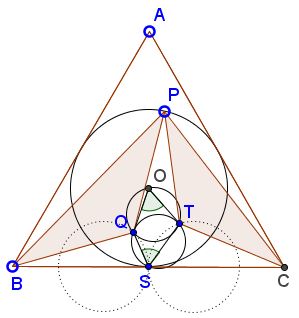
$\Delta QOT\;$ is the inner Napoleon triangle of $\Delta BCP\;$ so it is equilateral even if $\Delta ABC\;$ is not.
Acknowledgment
The problem that is due to Miguel Ochoa Sanchez has been posted by Leo Giugiuc at the CutTheKnotMath facebook page along with a solution by Leo Giugiuc and Dan Sitaru.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581196
