Archimedean Siblings out of Wedlock, i.e., Arbelos
What Might This Be About?
A few words
Two circles inscribed into arbelos as shown below, have been proved to be equal by Archimedes in Lemma 5 of his Book of Lemmas. For this reason, the two circles are known as the Archimedean twins.
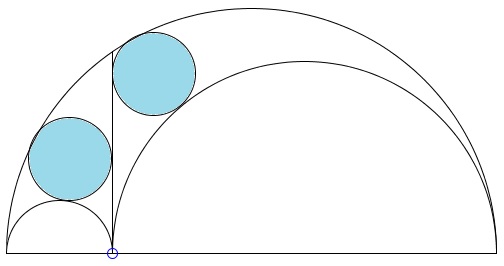
An arbelos is defined by three semicircles of, say, radii, $r_{1},$ $r_{2}$ and $r_{1}+r_{2}.$ The great Archimedes proved that the radius $r$ of his twins is defined by
(*)
$\displaystyle r=\frac{r_{1}r_{2}}{r_{1}+r_{2}}.$
Over few last decades several circles (usually in pairs), associated with arbelos, have been found to have the same radius. Every such circle is usually described as an Archimedean sibling, a twin (if it comes in a pair) or even one of a quadruplet. (An online catalog of Archimedean circles is maintained by the Dutch geometer Floor van Lamoen.)
There are other configurations where a pair of equal circles pops up. Some of the related theorems that tackle a pair of equal circles have been given rather descriptive names: the Eyeball theorem, the Praying Eyes theorem, the Squinting Eyes theorem, the Eye-to-Eye theorem, etc. Only recently the two configurations have been brought together. Continuing in this path of pursuing ophthalmological metaphor, Dao Thanh Oai and Emmanuel Antonio José García found additional Archimedean circle within and some outside, the arbelos.
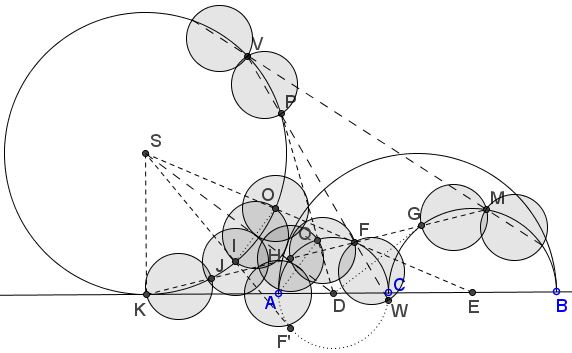
Below I explain the costruction of the new Archimedean siblings, mostly with just a reference to one of the ophthalmological theorems.
Construction
In our configuration, arbelos has point $C$ inside interval $AB.$ $(XY)$ will denote both the circle and a semicircle with diameter $XY.$ A circle with a known center, say $Z,$ will be denoted $(Z)$ if there is no ambiguity, or as $C(Z,W),$ where $W$ is a point on the circumference. Below, $(AC)=(D)$ and $(CB)=(E).$
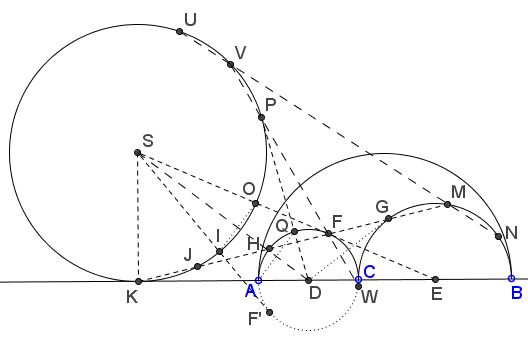
Draw $DG,$ $EF,$ tangent lines, with $G$ and $F$ being the points of tangency, as shown above. Let $K$ be the intersection of $AB$ with $FG,$ both produced. Extend $EF$ to meet the perpendicular to $AB$ at $S.$ Draw circle $(S)=C(S,K).$
$SF'$ is the second tangent to semicircle $(AC)$. $DP$ is the second tangent to $(S)$ from $D,$ with $P$ the point of tangency.
$I$ and $O$ are the intersections with $(S)$ of $SF'$ and $EF,$ respectively; $Q$ is the intersection of semicircle $AC$ with $DP;$ $J$ is the intersection of $FG$ and circle $(S);$ $H, M$ the second intersections of $FG$ with $(D)$ and $(E),$ respectively; $V,$ $W$ the second intersections of $FP$ with $(S)$ and $(D),$ respectively; $U$ and $N$ are the second intersections of $MV$ with $S$ and $E.$
- $X$ the midpoint of $IO,$ $Y$ the midpoint of $AQ.$
Now for the circles - the Archimedean siblings.
$(HF),$ $(GM)$ (These are García's Archimedean twins.)
$(KJ),$ $(HF)$ (Cross-eyed theorem.)
$(IO)$, $(AQ)$ (Focus on the Eyeball theorem, #7).
$C(I,X),$ $C(O,X),$ $C(A,Y),$ $C(Q,Y)$ (not shown) (Trivially, because $(IO)$, $(AQ)$ are Archimedean.)
$(VP),$ $(FW)$ (These are García's Archimedean twins.)
$(UV),$ $(MN)$ (Shedding Light on the Ball for Eyeballing.)
Acknowledgment
The above is a reproduction of a private mail message (August 29, 2014) by Emmanuel Antonio José García (Dominican Republic). Antonio has combined the discoveries of Dao Thanh Oai (Vietnam), Miguel Ochoa Sanchez (Peru), and his own into a tremendous collection of Archimedean circles.
- Arbelos - the Shoemaker's Knife
- 7 = 2 + 5 Sangaku
- Another Pair of Twins in Arbelos
- Archimedes' Quadruplets
- Archimedes' Twin Circles and a Brother
- Book of Lemmas: Proposition 5
- Book of Lemmas: Proposition 6
- Chain of Inscribed Circles
- Concurrency in Arbelos
- Concyclic Points in Arbelos
- Ellipse in Arbelos
- Gothic Arc
- Pappus Sangaku
- Rectangle in Arbelos
- Squares in Arbelos
- The Area of Arbelos
- Twin Segments in Arbelos
- Two Arbelos, Two Chains
- A Newly Born Pair of Siblings to Archimedes' Twins
- Concurrence in Arbelos
- Arbelos' Morsels
![]()
Related material
| |
Problems with Ophthalmological Connotations | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73534615
