Shedding Light on the Ball for Eyeballing

E. A. J. García
27 June, 2014

Recall Dao's Eyeballing a Ball problem.

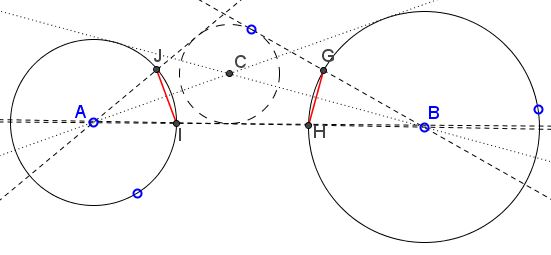
Eyeballing a Ball - problem

In this case the segments $IJ,$ $GH$ are not necessarily congruent to those segments corresponding to the Praying Eyes Theorem. So, one would ask: when segments $IJ,$ $GH$ are equal to those of the Praying Eyes Theorem? Well, Ochoa has answered the question by misinterpreting Dao's problem.

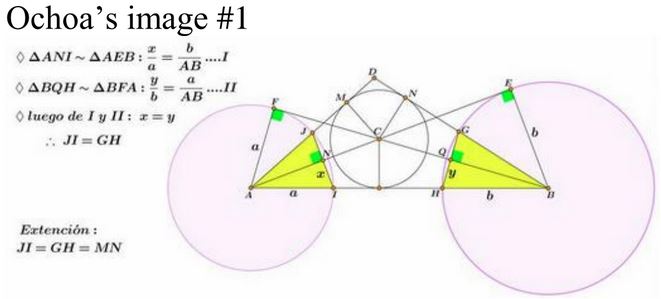
ssshedding light on Eyeballing a Ball problem, 1

In Ochoa's image at CTK-Facebook, he takes $ABD$ as a triangle with $C$ as its incenter, which is different from Dao's configuration. Ochoa also stated that $MN$ equals $IJ = GH.$

Now I will prove that $IJ = GH = MN,$ but I will change the notations.

Consider two circles $(A),$ $(C).$ From $A$ draw a line tangent to $(C)$ at $I.$ From $C$ draw a line tangent to $(A)$ at $J.$ Let $E$ be the intersection of $AI$ and $CJ.$ Draw a circle centered at $E$ and tangent to $AC$ at $F.$ Now, from $A$ draw a line tangent to $(E)$ at $G$ and from $C$ draw another line tangent to $(E)$ in $H.$ Let $K$ be the intersection of $AG,$ $CH.$

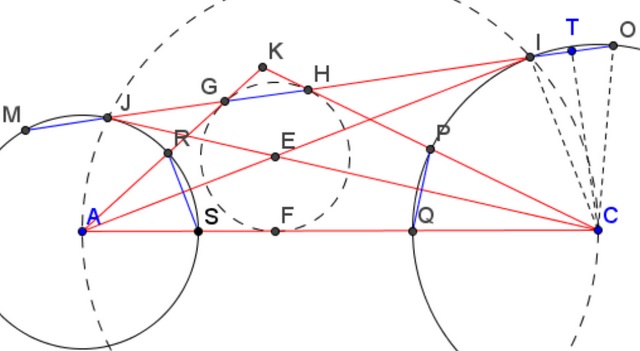
ssshedding light on Eyeballing a Ball problem, 2

Let $CT\perp IO.$

$\begin{align} \angle TIC&=180^{\circ}-90^{\circ}-\angle JIA=90^{\circ}-\angle JIA,\\ \angle TCI&=90^{\circ}-(90^{\circ}-\angle JIA)=\angle JIA=\angle JCA,\\ \angle ECF &=\angle HCE, \end{align}$

so $CP=CQ,$ implying $CE\perp PQ.$

It follows easily that triangles $COI$ and $CPQ$ are congruent and therefore $OI = PQ.$

Now I will prove that $G,$ $H$ are on segment $IJ.$

Let $ACK$ be a triangle with $E$ as the incenter. Let $FGH$ be the intouch triangle of $ACK.$ Let the bisector $AE$ intersect circle $(CHEF)$ in $I.$

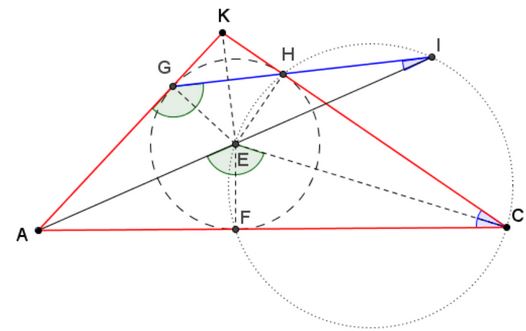
ssshedding light on Eyeballing a Ball problem, 3

Then $G,$ $H,$ $I$ are collinear.

Indeed,

$\begin{align} \angle AKC&=180^{\circ}-\angle KAC-\angle KCA,\\ \angle KGH&=(180^{\circ}-\angle AKC)/2, \\ \angle KGH&=\angle KAC/2+\angle KCA/2,\\ \angle AGH&=180^{\circ}-\angle KAC/2-\angle KCA/2,\\ \angle AEC&=180^{\circ}-\angle KAC/2-\angle KCA/2. \end{align}$

Hence, $\angle AGH=\angle AEC.$

Also, $\angle EIH = \angle ACE.$ So, $AEIG$ is a triangle and is similar to $\Delta AEC.$ Which means that $H$ is on $GI$ and therefore, $G,$ $H,$ $I$ are collinear.

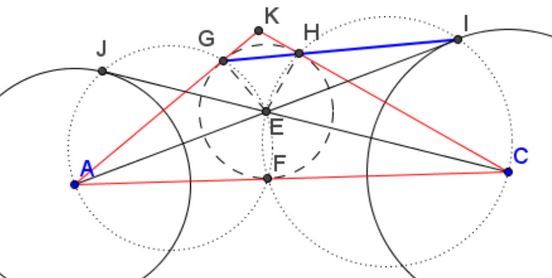
ssshedding light on Eyeballing a Ball problem, 4

Analogously, $G$, $H,$ $J$ are also collinear and, therefore, $G,$ $H$ are on $IJ.$ Further,

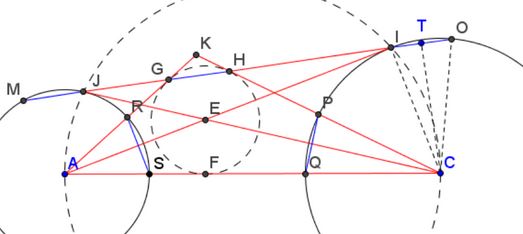
ssshedding light on Eyeballing a Ball problem, 5

$MJ = GH$ [Praying Eyes Theorem wrt circles $(A),$ $(E)$],
$IO = GH$ [Praying Eyes Theorem wrt circles $(C),$ $(E)$],
$MJ = IO$ [Praying Eyes Theorem wrt circles $(A),$ $(C)$].

Summarizing:

$MJ = IO = GH = PQ = RS.$

So now, in order to understand Ochoa's image associated to the Archimedean circles consider the case where semicircles $(A),$ $(C)$ are tangent as in arbelos. As $MJ = IO = GH = PQ = RS$ and $MJ = IO = 2R_{a}R_{c}/(R_{a} + R_{c}),$ we will have a new triplet of Archimedean circles.

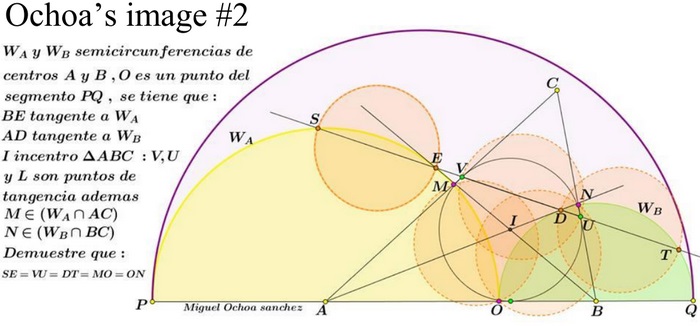
ssshedding light on Eyeballing a Ball problem, Archimedean triplet

Related material
Read more...

Problems with Ophthalmological Connotations

  • The Eyeball Theorem
  • Eye-to-Eye Theorem I
  • Eye-to-Eye Theorem II
  • The Squinting Eyes Theorem
  • Eyeballing a ball
  • Praying Eyes Theorem
  • Focus on the Eyeball Theorem
  • Eyeball Theorem Rectified
  • Bespectacled Eyeballs Extension
  • Eyeballs Projected
  • Archimedean Siblings out of Wedlock, i.e., Arbelos
  • Rectified, Halved, Sheared, Eyeballs Still Surprise

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    73361764