Bespectacled Eyeballs Extension
What is this about?
Problem
Circle $O(I)$ and $O(J)$ are centered at $O$ and are through $I$ and $J,$ respectively. Circle $Q(K)$ and $Q(L)$ are centered at $Q$ and are through $K$ and $L,$ respectively. $OL$ and $OL'$ are tangent to $Q(L);$ $QI$ and $QI'$ are tangent tangent to $O(I).$ Further, $J=OL\cap O(J),$ $G=OL'\cap O(J),$ $K=QI\cap Q(K),$ $H=OI'\cap Q(K).$ Also, $\displaystyle\frac{OI}{OJ}=\frac{QL}{QK}.$
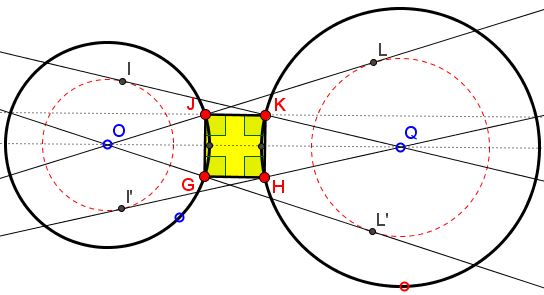
Prove that $GHKJ$ is a rectangle.
Solution
Observe that when the given ratio is $1$ the problem reduces to the Eyeball theorem. Define $J'=OL\cap O(I),$ $G'=OL'\cap O(I),$ $K'=QI\cap Q(L),$ $H'=OI'\cap Q(L).$
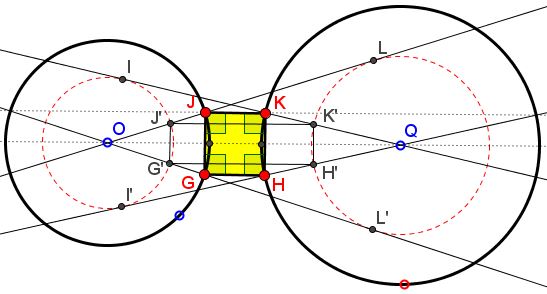
Then, by the Eyeball theorem, $G'H'K'J'$ is a rectangle. From $\displaystyle\frac{OI}{OJ}=\frac{QL}{QK}$ we also have $\displaystyle\frac{J'G'}{JG}=\frac{K'H'}{KH}$ while, due to symmetry, $J'G'\parallel JG$ and $K'H'\parallel KH.$ This implies that $GHKJ$ is also a rectangle.
(This is an example of a problem in which a particular case implies the more general one.)
Acknowledgment
The above has been submitted by Dao Thanh Oai (Vietnam) in private communication.
Related material
| |
Problems with Ophthalmological Connotations | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73575019
