Eye-to-Eye Theorem II
What is this about?
Problem
$(A)$ and $(B)$ are two non-intersecting circles, with the internal center of similarity at $C.$ $(C)$ any circle with the radius less than $AC$ and $BC.$ From $A$ and $B$ draw tangents to $(C)$ and mark points $M,N,I,H$ and $G,J,P,O$ where they intersect circles $(A)$ and $(B),$ respectively.
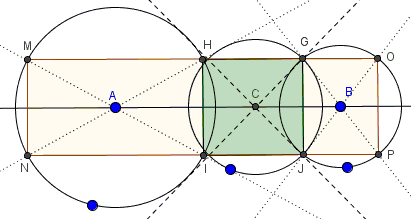
Then points $M,H,G,O$ are collinear as are points $N,I,J,P;$ both lines are parallel to $AB,$ making several rectangles, say, $HIJG$ and $MNPO.$
Hint
There is a good deal of tangent lines and, hence, right triangles. Some of these are similar.
Solution 1
I shall prove the assertion only for $HIJG.$
Let $E$ be the foot of the perpendicular from $H$ to $AB;$ $K,L,M,N$ points of tangency, as shown in the diagram:$
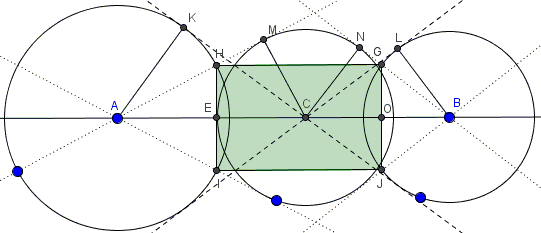
Triangles $AEH$ and $AMC$ are right and similar because they share an acute angle at $A.$ We have the proportion: $EH/AH=CM/AC$ from which
$\displaystyle EH=R_{C}\frac{R_A}{AC},$
where $R_A$ and $R_C$ are the radii of $(A)$ and $(C),$ respectively. Similarly, for the foot of perpendicular $O$ from $G,$
$\displaystyle GO=R_{C}\frac{R_B}{BC},$
where $R_B$ is the radius of $(B).$
Finally, triangles $ACK$ and $BCL$ are similar due to the choice of $C.$ We have the proportion: $AK/AC=BL/BC,$ i.e., $R_{A}/AC=R_{B}/BC.$ Combining the three proportions shows that $EH=GO.$
Solution 2
Dao Thanh Oai has informed of another solution which is based on a double application of the Eyeball theorem:
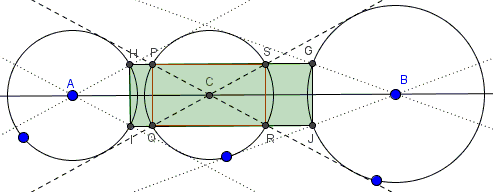
One application of the Eyeball theorem shows that $HIQP$ is a rectangle, the other that $SRJG$ is another one. The fact that $PQRS$ is a rectangle due to the central symmetry of diameters $PR$ and $QS$ in circle $(C).$
Acknowledgment
The problem arouse as a generalization of the one I dubbed Eye-to-Eye Theorem I and is entitled to the moniker of Eye-to-Eye Theorem II.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73518506
