Eyeballs Projected
What is this about?
Problem
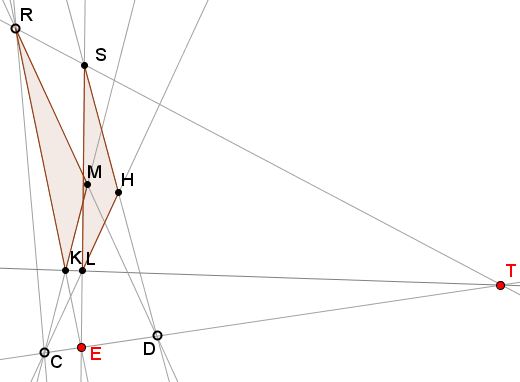
In the projective plane, let $C$ and $D$ be points on the line $AB,$ let $G$ and $H$ be points not on the line, let $AG\cap DH = S,$ $CG\cap BH = R,$ $AH\cap GD = K,$ $BG\cap CH = L,$ $RD\cap CK = M,$ $CS\cap DL = N,$ $AH\cap CG = I$ and $BG\cap HD = J.$
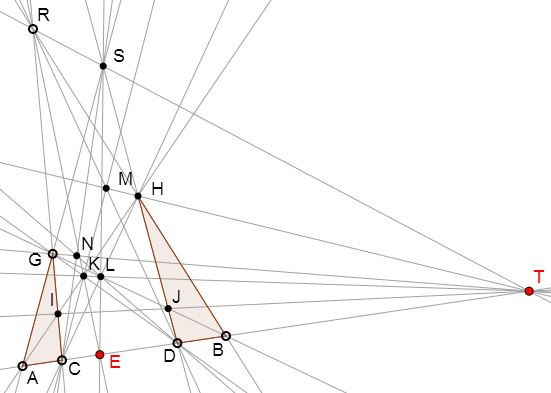
Then the lines $MH,$ $GN,$ $KL,$ $IJ$ and $AB$ are concurrent.
Lines $AB,$ $RK$ and $SL$ are also concurrent.
Solution
HM
Consider the triangles $AGC$ and $HDM$ which are in perspective from $K.$
Since $AG \cap HD = S$ and $CG \cap MD = R,$ Desargues' theorem gives $AC \cap HM = T$ as required. And, by symmetry, $BD \cap GN = T.$
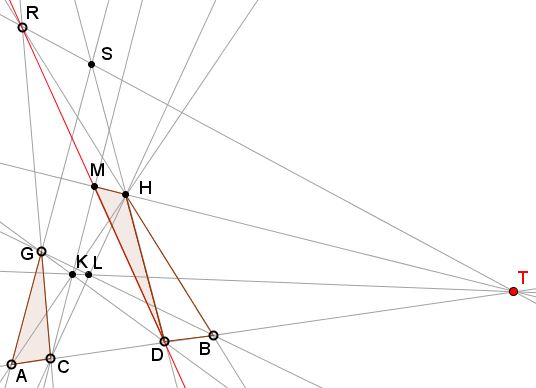
KL
Consider the triangles $GKC$ and $BTH.$ Since $KG \cap BT = D, $ $GC \cap BH = R$ and $CK \cap TH = M$ are collinear, the converse of Desargues' theorem implies that the triangles are in perspective from $CH \cap BG = L$ so $KT$ passes through $L$ as required.
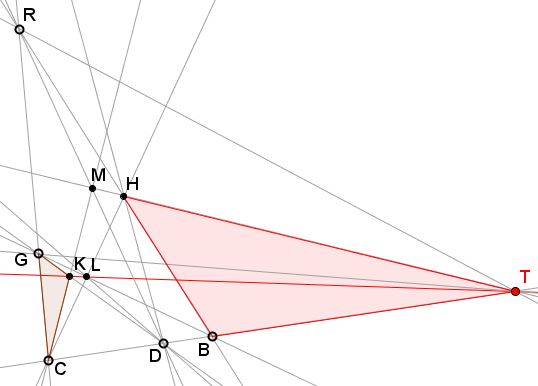
IJ
Since I have not found a proof similar to the above, I refer to the proof in an earlier page and give a projective version of the similar triangles calculation. Let $S' = AH \cap ST $, $H' = RB \cap GT $, $D' = SH' \cap AB,$ $I'=AH'\cap CR,$ $J' = GB \cap SH',$ and $S'' = AH' \cap ST.$
It is clear from the proof referred to that $I'J'T$ are collinear so project $S'HIA \rightarrow ^{R} S''H'I'A \rightarrow ^{T} SH'J'D' \rightarrow ^{B} SHJD $. Since it is known that a projectivity is defined by the images of three of the points, the composite projectivity is a projection from $S'HA$ to $SHD$ using $T$ and must therefore take $I$ to $J$.
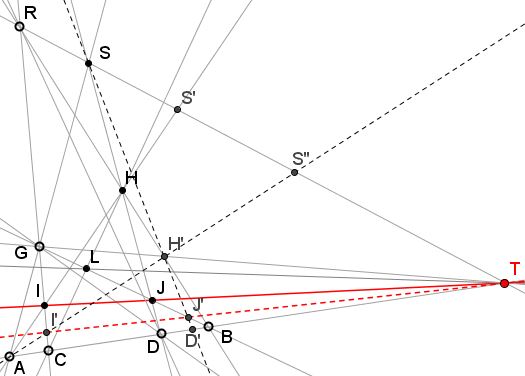
E
To show that $E = RK \cap SL$ is on $AB$, look at triangles $SHL$ and $RMK$ that are in perspective from $T.$ Corresponding sides intersect in $D = SH \cap RM$, $C = MK \cap HL$ and $E = SL \cap RK$ which are therefore collinear.
IJ again
The point $E$ plays an important role as will be seen in this attempt to find a more direct proof.
Let $S' = AK \cap ST$ and $R' = BL \cap RT$, then $AIKS' \rightarrow ^{R} ACET$ and $BJLR' \rightarrow ^{S} BDET$.
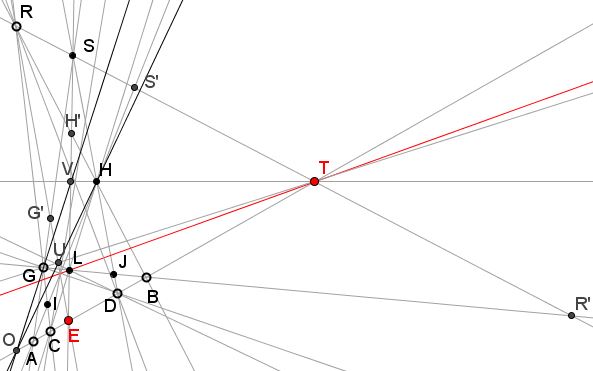
If it can be shown that the cross ratios $ACET$ and $BDET$ are the same, then, since $AKS' \rightarrow ^{T} BLR',$ $IJT$ will be collinear. Let $G'= AS \cap ER,$ $H'= BR \cap ES,$ $U = GT \cap ER,$ $V = HT \cap ES$ and $O = GV \cap AE.$ It remains to prove that $GV \cap AB = O$ because Desargues' theorem then shows that $UH \cap AB = O$ also and, in the case when $RT$ is the line at infinity, the triangular configurations $AEUG'G$ and $EBHH'V$ are similar so the equality of the cross ratios is then a similar triangles calculation.
Acknowledgment
The above statement and proof are due to Hubert Shutrick, who from the beginning insisted that the whole of the theorem on the Rectified, Halved, Sheared, Eyeballs Still Surprise page belongs to projective geometry.
The dynamic illustration shows that the whole of the initial theorem ought to have projective nature and, along the way, strengthens the statement.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578563
