The Eyeball Theorem: What Is It?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny

The applet suggests the following statement:

The Eyeball Theorem

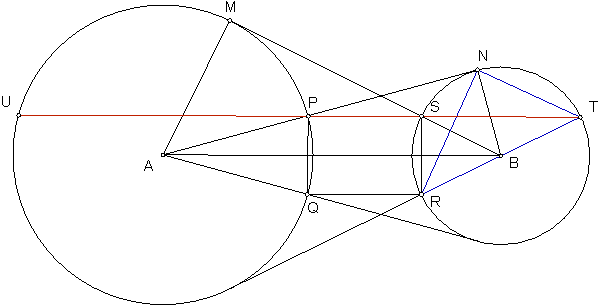
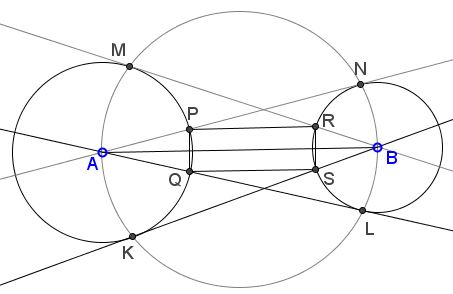
Let there be two circles C(A, RA) and C(B, RB), one with center A and radius RA, the other with center B and radius RB. Assume the tangents from A to C(B, RB) intersect C(A, RA) at points P and Q, whereas the tangents from B to C(A, RA) intersect C(B, RB) at points R and S. Then PQ = RS.

Proof 1

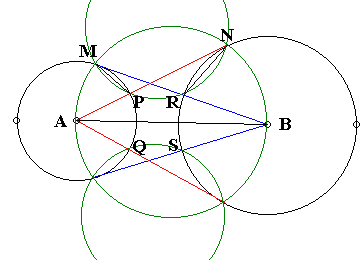
Angles AMB and ANB are right. Therefore, the quadrilateral AMNB is cyclic, which implies

(1)	∠MAN = ∠MBN,

since the two angles subtend the same arc. Now,

∠PMR = ∠MAP/2 (= ∠MAN/2) ∠PNR = ∠RBN/2 (= ∠MBN/2)

since the two angles are formed by a tangent and a chord. Along with (1) this gives

(2)	∠PMR = ∠PNR,

which means that the quadrilateral MPRN is also cyclic. From here,

(3)	∠NMR = ∠NPR,

while, for a similar reason in the circle circumscribing the quadrilateral AMNB,

(4)	∠NAB = ∠NMB (= ∠NMR),

so that from (3) and (4) we conclude that

∠NPR = ∠NAB.

In other words, PR is parallel to AB. Since PQ ⊥ AB and RS ⊥ AB, and because of the symmetry in AB, the quadrilateral PQSR is a rectangle, so that PQ = RS, indeed.

Proof 2

(NRich Program, University of Cambridge)

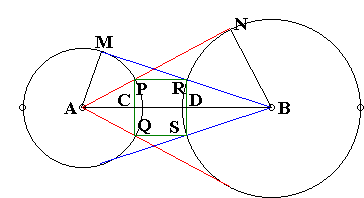
Let C be the midpoint of PQ. C lies on AB, and therefore ΔACP is right. As such, it is similar to the right triangle ANB, since the two share an angle. From the similarity of the triangles we derive the proportion CP/AP = BN/AB, which means that

(5)	CP = RARB/AB, or PQ = 2·RARB/AB

The latter expression is symmetric in A and B. Therefore also RS = 2·R_AR_B/AB. Q.E.D.

Proof 2'

We could have used (5) a little differently. Assume the circle C(A, R_A) is fixed as is the point B. What happens when R_B changes? Obviously (or, e.g., because all circles are similar), DR, where D is the center of RS, changes linearly in proportion to R_B. From (5), the same is true of CP. The rates are bound to be the same, since when R_A = R_B, we trivially have CP = DR. Therefore, the latter identity holds for any R_B.

Proof 3

(E. J. Barbeau, M. S. Klamkin, W. O. J. Moser, Problem 185)

Triangles AMU and BNU are similar, from which

On the other hand, AM = AP and BN = BR, such that (6) implies

Floor van Lamoen has suggested a different ending following (6'). The latter says that PR is parallel to AB as P and R divide the sides AU and BU of triangle ABU in the same ratio. The same holds for QS: QS||AB. It follows that QSRP is a rectangle which proves the theorem.

He also came up with an entirely novel proof, which, although, lengthy brings to light additional features of the configuration:

(By Floor van Lamoen, March 2006, private communication)

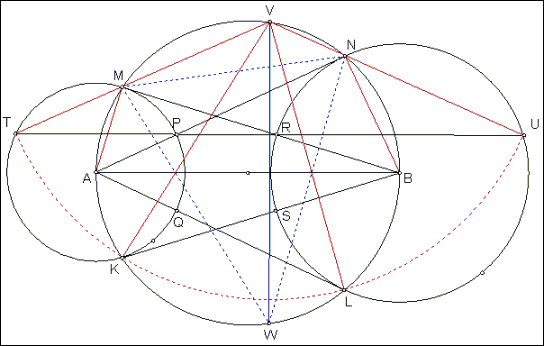
Extend PR to TU with T on circle A and U on circle B. Let TM and UN meet in V.

Note that ∠MAN = ∠MBN and thus

so triangle TUV is isosceles with VT = VU.

We also see that

so that ∠MBN) and ∠NVM add to 180 degrees, so that V lies on the circle with diameter AB.

Since inscribed angles TVA and KVA subtend equal arcs they are equal: ∠TVA = ∠KVA and, similarly, ∠UVB = ∠LVB. By reflection through AV and BV respectively, we see that in fact VT = VK = VL = VU.

Let W be the reflection of V through AB. ΔWMN is isosceles just as ΔKLV. Hence

so VW bisects angle TVU, and VW is perpendicular to PR, and thus PR is parallel to AB. By symmetry PQSR is a rectangle.

Proof 5

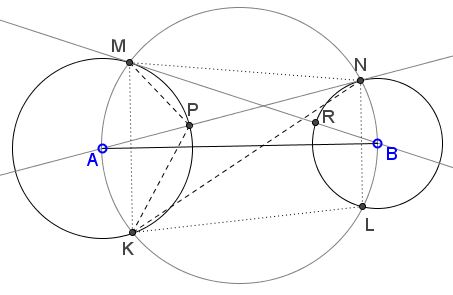
Talk about the length of a proof. Here is quite a short one also by Floor van Lamoen (private communication, March 28, 2006):

With a reference to the following diagram

Note that ∠RNA = ∠RTN by inscribed angles.

By isosceles ΔNBR, ∠BNR = ∠BRN.

So

This shows that TR is a diameter of circle (B). Hence ∠RST is right. By symmetry PQRS is a rectangle.

Remark 1

The last proof makes an unwarranted assumption. Can you locate it?

Remark 2

(There is another interesting fact with ophthalmological connotations that I dubbed the Squinting Eyes Theorem.)

References

1. E. J. Barbeau, M. S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges, MAA, 1995
2. J. Konhauser, D. Velleman, S. Wagon, Which Way Did the Bicycle Go?, MAA, 1996, #33
3. D. Wells, Curious and Interesting Geometry, Penguin Books, 1991

|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny