Garcia's Archimedean Quadruplets

What Might This Be About?

Problem

Semicircles $(D)$ and $(E)$ are drawn on diameters $AC$ and $BC,$ respectively, $C$ being a point on segment $AB.$ $EF$ is tangent to $(D),$ $DG$ is tangent to $(E).$ Line $FG$ intersects $(D)$ second time in $H$ and $(E)$ in $I.$

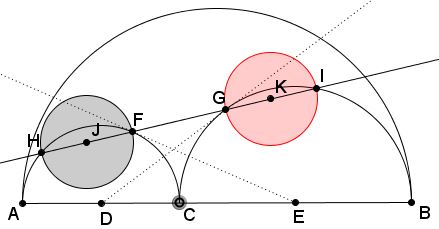
Garcia's Archimedean twins - problem

The two circles on $FH$ and $GI$ as diameters are Archimedean twins, i.e. have the radius equal to that of the pair of circles discovered by Archimedes.

Proof

If $R_{1}$ and $R_{2}$ are the radii of $(D)$ and $(E),$ then it is known that the radius of the Archimedean circles equals $\displaystyle R=\frac{R_{1}R_{2}}{R_{1}+R_{2}}.$ To prove that this is the case in the present setup use the similarity of triangles $EGK$ and $DEF.$ (This and other ancillary assertions have either been proved on an earlier page or are an easy consequence of the latter.)

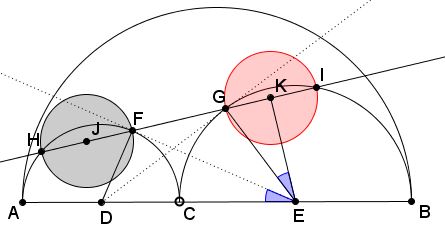
Garcia's Archimedean twins - solution

We have the proportion: $\displaystyle \frac{GK}{EG}=\frac{DF}{DE},$ i.e., $\displaystyle \frac{R}{R_{2}}=\frac{R_{1}}{R_{1}+R_{2}},$ thus proving the claim.

Extra Pair

Define $L$ to be the intersection of $DG$ with $(D)$ and $M$ the intersection of $EF$ with $(E),$ $L'$ and $M'$ their reflections in $AB.$

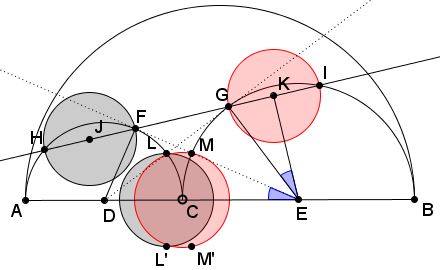
Garcia's Archimedean twins - Extra

Then the circles on $LL'$ and $MM'$ as diameters are also Archimedean.

The proof is a consequence of Item #7 on the aforementioned page.

Extra++

Define $F'$ and $G'$ as reflections of $F$ and $G$ in $AB.$ This makes $EF'$ tangent to $(D)$ and $DG'$ to $(E).$ Let $H'$ be the second intersection of $FG'$ with $(D);$ $I'$ the second intersecion of $GF'$ with $(E).$

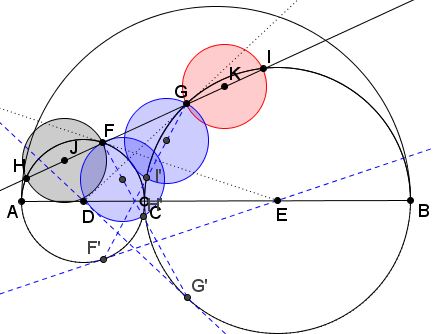
Garcia's Archimedean third pair of twins

Then the circles on $FH'$ and $GI'$ as diameters are also Archimedean.

The fact is a consequence of the second case of the Praying Eyes theorem.

Acknowledgment

All the observations and results on this page are due to Emmanuel Antonio José García (Dominican Republic).

71945892