Praying Eyes Theorem
What is this about?
Problem
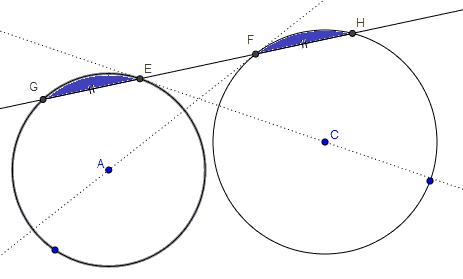
Let $AF$ and $CE$ be tangent to circles $(A)$ and $(C),$ as shown below.
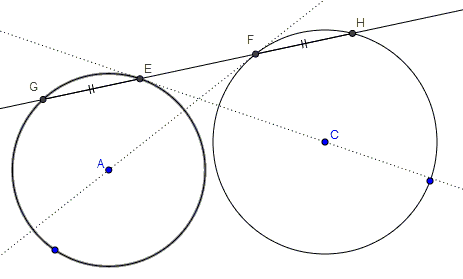
Let $EF$ intersect the second time $(A)$ in $G$ and $(C)$ in $H.$ Then $EG=FH.$
Hint
Think of the Power of a Point theorem and drawing ancillary tangents. The Pythagorean theorem may also prove useful.
Solution
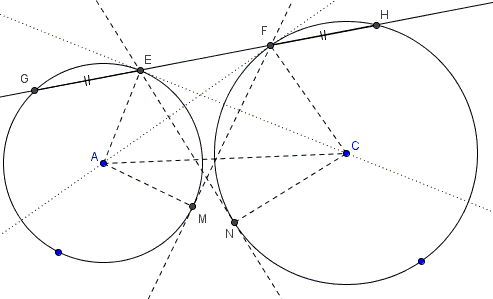
Draw tangents $EN$ to $(B)$ and $FM$ to $(A).$ These happen to be equal. Indeed, by several applications of the Pythagorean theorem:
$ \begin{align} EN^{2} &= CE^{2}-CN^{2} & (\mbox{from right}\space\Delta CEN) \\ &= AC^{2}-AE^{2}-CN^{2} & (\mbox{from right}\space\Delta ACE) \\ &= AC^{2}-R_{A}^{2}-R_{C}^{2} & (\mbox{radii of}\space (A)\mbox{and}\space (C)) \\ &= AC^{2}-R_{C}^{2}-R_{A}^{2} & \\ &= AC^{2}-CF^{2}-AM^{2} & \\ &= AF^{2}-AM^{2} & (\mbox{from right}\space\Delta ACF) \\ &= FM^{2} & (\mbox{from right}\space\Delta AFM). \end{align} $
Thus, $EN=FM.$ Now, by the Power of a Point theorem, $FM^{2}=FE\cdot FG$ and also $EN^{2}=EF\cdot EH.$ It follows that $FE\cdot FG=EF\cdot EH$ and, therefore, $FG=EH.$ Finally,
$EG=FG-EF=EH-EF=FH,$
as required.
A Second Case
There is a second case where line $EF$ crosses the line of centers $AC.$ I intentionally duplicate the notations from the previous case and its proof to make it clear that the proof stands in the new case as well.
Let $AF$ and $CE$ be tangent to circles $(A)$ and $(C),$ as shown below.
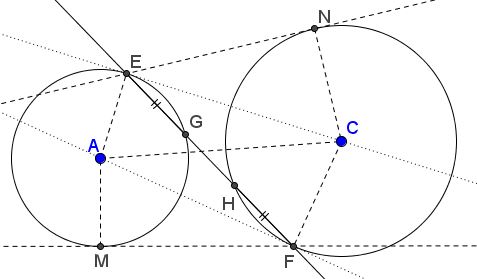
Let $EF$ intersect the second time $(A)$ in $G$ and $(C)$ in $H.$ Then $EG=FH.$
$ \begin{align} EN^{2} &= CE^{2}-CN^{2} & (\mbox{from right}\space\Delta CEN) \\ &= AC^{2}-AE^{2}-CN^{2} & (\mbox{from right}\space\Delta ACE) \\ &= AC^{2}-R_{A}^{2}-R_{C}^{2} & (\mbox{radii of}\space (A)\mbox{and}\space (C)) \\ &= AC^{2}-R_{C}^{2}-R_{A}^{2} & \\ &= AC^{2}-CF^{2}-AM^{2} & \\ &= AF^{2}-AM^{2} & (\mbox{from right}\space\Delta ACF) \\ &= FM^{2} & (\mbox{from right}\space\Delta AFM). \end{align} $
Thus, $EN=FM.$ Now, by the Power of a Point theorem, $FM^{2}=FE\cdot FG$ and also $EN^{2}=EF\cdot EH.$ It follows that $FE\cdot FG=EF\cdot EH$ and, therefore, $FG=EH.$ Finally (and here is the only difference with the first case),
$EG=EH-GH=FG-GH=FH,$
as required.
The Two Cases Together
We found that the identity $EG=FH$ holds in the two cases. It is interesting to see whether the length of the segments is the same in both cases. In fact, there is an equality. (Now that both cases need to be depicted in the same diagram, the symbols for the points in the second case are decorated with an apostrophe:
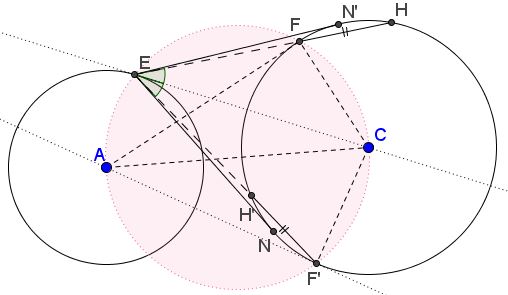
By the construction, $\angle AEC=\angle AF'C=\angle AFC,$ implying that points $E,F,F'$ lie on the circle with diameter $AC.$ Further $\angle CEF=\angle CEF'$ since both those angles are subtended by equal chords $(CF=CF').$ Also, since $EN$ and $EN'$ are two tangents from $E$ to $(C),$ $\angle CEN=\angle LEN';$ it follows that $\angle FEN'=\angle F'EN$ such that the chords $FH$ and $F'H'$ are equally inclined to the tangents from the same point. The two are, therefore, equal: $FH=F'H'.$
Acknowledgment
The problem with solution has been posted by Emmanuel Antonio José García at the CutTheKnotMath facebook page.
I named it the "Praying Eyes" theorem because of the association (which I shall explore on a separate page) with the Eyeball Theorem.
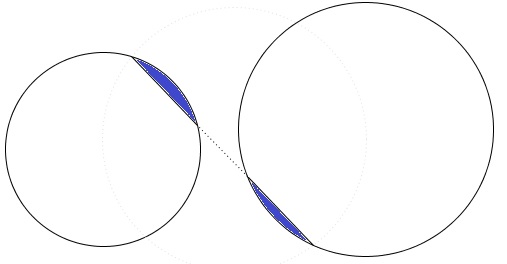
Although, perhaps, the second case deserves a designation as a "Cross-eyed theorem":
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73585943
