Eye-to-Eye Theorem I

What is this about?

Problem

$(A)$ and $(B)$ are two circles tangent externally at $C.$ $(C)$ any circle with the radius less than $AC$ and $BC.$ From $A$ and $B$ draw tangents to $(C)$ and mark points $E,G,N,L$ and $F,H,O,M$ where they intersect circles $(A)$ and $(B),$ respectively.

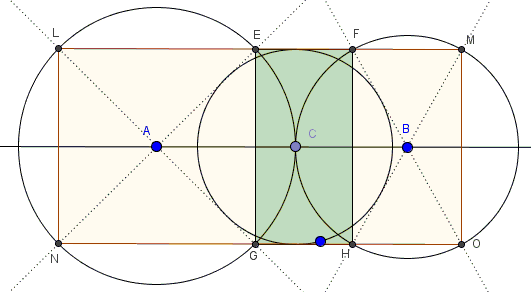
Eye-to-Eye theorem I - problem

Then points $L,E,F,M$ are collinear as are points $N,G,H,O;$ both lines are parallel to $AB,$ making several rectangles, say, $EGHF$ and $LNOM.$

Hint

There is a good deal of tangent lines and, hence, right triangles. Some of these are similar.

Solution

I shall prove the assertion only for $EGHF.$

Let $I$ be the foot of the perpendicular from $E$ to $AB;$ $J$ the point of tangency of $AE$ and $(C).$

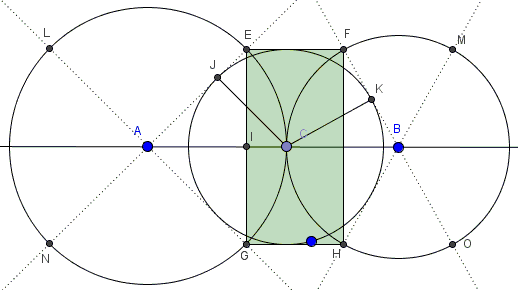
Eye-to-Eye theorem I - solution

Triangles $AEI$ and $ACJ$ are right and similar because they share an acute angle at $A.$ Their hypotenuses $AC$ and $AE$ are equal as radii of $(A).$ It follows that $\Delta AEI=\Delta ACJ$ and, hence, $EI=CJ$ - the radius of $(C).$

By symmetry, the same holds for $G,F,H,$ making $EGHF$ a rectangle with sides $EF$ and $GH$ tangent to $(C).$

Acknowledgment

The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.

The statement admits an easy generalization. I took the liberty of naming the two Eye-to-Eye theorem I and Eye-to-Eye Theorem II.

Related material
Read more...

Problems with Ophthalmological Connotations

  • The Eyeball Theorem
  • Eye-to-Eye Theorem II
  • The Squinting Eyes Theorem
  • Eyeballing a ball
  • Praying Eyes Theorem
  • Focus on the Eyeball Theorem
  • Eyeball Theorem Rectified
  • Bespectacled Eyeballs Extension
  • Shedding Light on the Ball for Eyeballing
  • Eyeballs Projected
  • Archimedean Siblings out of Wedlock, i.e., Arbelos
  • Rectified, Halved, Sheared, Eyeballs Still Surprise

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    71867957