Rectified, Halved, Sheared, Eyeballs Still Surprise
What is this about?
Problem
Similar triangles $ACG$ and $DBH$ share the base line $AB.$ $I=CG\cap AH,$ $J=BG\cap DH,$ $K=DG\cap AH,$ $L=BG\cap CH.$
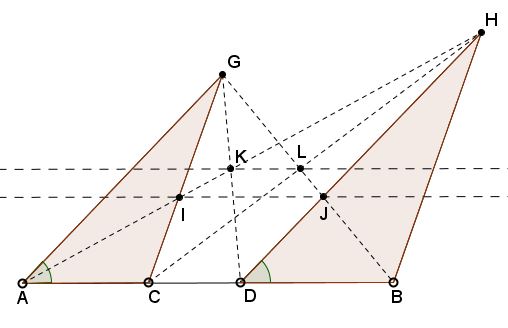
Prove that $IJ\parallel AB\parallel KL.$
Solution
The fact that $KL\parallel AB$ has a projective analogue that is easily solved with Thales' theorem.
Concerning $IJ$ also being parallel to $AB,$ note that if the triangles $ACG$ and $DBH$ are equal, the claim is rather simple.
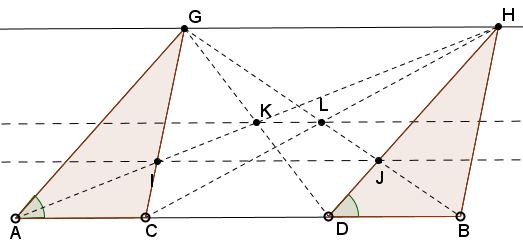
Triangles $ACI$ and $HGI$ are similar, implying $\displaystyle\frac{CI}{GI}=\frac{AC}{GH}.$ Triangles $BDJ$ and $GHJ$ are also similar, implying $\displaystyle\frac{DJ}{HJ}=\frac{BD}{GH}.$ But if $\Delta ACG=\Delta DBH,$ $AC=BD$ so that $\displaystyle\frac{CI}{GI}=\frac{DJ}{HJ}.$ By Thales' theorem, $IJ\parallel AB.$
In the general case, choose $D'$ on $AB$ such that $D'B=AC$ and make $D'H'\parallel DH,$ with $H'$ on $BH.$ Define $I'$ and $J'$ accordingly. We just saw that $I'J'\parallel AB.$
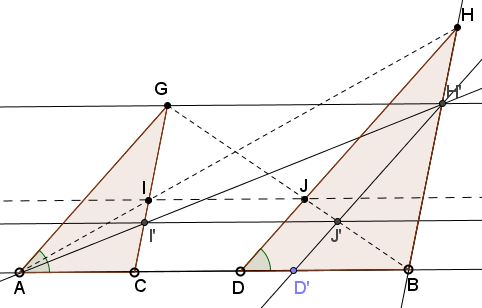
From a several pairs of similar triangles,
$\displaystyle\frac{AI}{HI}=\frac{AI'}{HI'}=\frac{D'J'}{H'J'}.$
Also
$\displaystyle\frac{D'J'}{DJ}=\frac{BJ'}{BJ}=\frac{H'J'}{HJ}$
so that
$\displaystyle\frac{D'J'}{H'J'}=\frac{DJ}{HJ},$
implying
$\displaystyle\frac{AI}{HI}=\frac{DJ}{HJ},$
and (from $\Delta ADH$) making $IJ\parallel AB.$
Acknowledgment
The is the extension of the Eyeball Theorem Rectified problem first suggested by Machó Bónis $(IJ)$ and then augmented by Dao Thanh Oai $(KL).$
Leo Giugiuc came up with a short analytic solution.
Hubert Shutrick has been insisting that the whole statement is of projective nature. He came up with a convincing dynamic illustration that I placed in a separate file.
Related material
| |
Problems with Ophthalmological Connotations | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73580349
