Eyeballing a Ball

What is this about?

Problem

$(A)$ and $(B)$ are two non-intersecting circles. $C$ is one of the points of intersection of the tangents from $A$ to $(B)$ with those from $B$ to $(A).$ $(C)$ is a circle with center $C.$ The tangents form $A$ to $(C)$ intersect $(A)$ in $I$ and $J.$ The tangents form $B$ to $(C)$ intersect $(B)$ in $G$ and $H.$

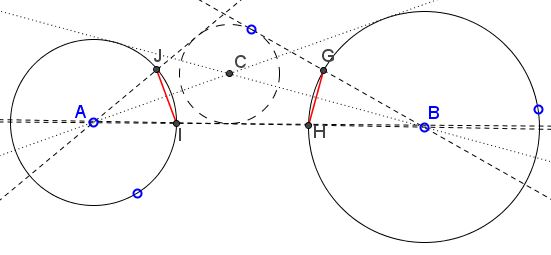
Eyeballing a Ball - problem

Prove that $IJ=GH.$

Hint

Not for nothing the problem's caption reads "Eyeballing a ball." This is to remind of the Eyeball theorem.

Solution

$C$ lies at the intersection of tangents from $A$ to $(B)$ and from $B$ to $A.$ For the two lines therefore could be looked at as the tangents from $C$ to $(A)$ and $(B).$ Note that the vertical angles the two lines form are equal. Add the missing pair of the tangents from $C$ to $(A)$ and $(B).$

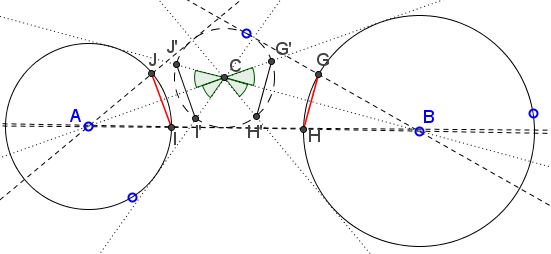
Eyeballing a Ball - solution

Denote the points of intersction of the tangents from $C$ $I',J',G',H',$ as in the above diagram. By the Eyeball theorem, $IJ=I'J'$ and $GH=G'H'.$ By the remark about the vertical angles, their doubles are also equal: $\angle I'CJ'=\angle G'CH',$ making the subtending chords equal: $I'J'=G'H'.$ This proves the statement.

Acknowledgment

The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page; the solution is by Emmanuel Antonio José García (Dominican Republic).

Related material
Read more...

Problems with Ophthalmological Connotations

  • The Eyeball Theorem
  • Eye-to-Eye Theorem I
  • Eye-to-Eye Theorem II
  • The Squinting Eyes Theorem
  • Praying Eyes Theorem
  • Focus on the Eyeball Theorem
  • Eyeball Theorem Rectified
  • Bespectacled Eyeballs Extension
  • Shedding Light on the Ball for Eyeballing
  • Eyeballs Projected
  • Archimedean Siblings out of Wedlock, i.e., Arbelos
  • Rectified, Halved, Sheared, Eyeballs Still Surprise

    • |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    72084247