Focus on the Eyeball Theorem
What is this about?
Problem
Let $AF$ and $CE$ be tangent to circles $(A)$ and $(C),$ as shown below. Let $EF$ intersect the second time $(A)$ in $G$ and $(C)$ in $H.$ $AF$ crosses $(A)$ at $I,$ $CE$ crosses $(C)$ at $L.$ $J$ and $K$ are symmetric images of $I$ and $L,$ respectively, in $AC.$
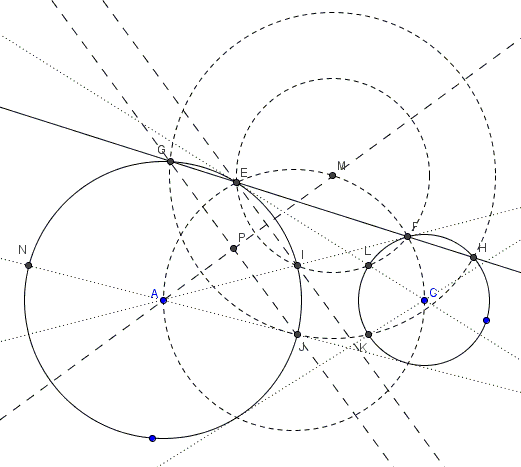
The following properties (some from the Eyeball theorem, some from the Praying Eyes Theorem, some are new) hold:
Points $A,E,F,C$ are concyclic (Proof #1 of the Eyeball theorem),
Points $E,I,L,F$ are concyclic (Proof #1 of the Eyeball theorem),
Center $M$ of $(EILF)$ lies on $(AEFC),$
The tangent to $(AEFC)$ at $M$ is parallel to $EF.$
$IJ=LK$ (the Eyeball theorem),
$GE=FH$ (the Praying Eyes Theorem),
$IJ=GE=FH=LK,$
$IL\parallel AC$ (the Eyeball theorem),
$EI\parallel GJ \parallel CM,$
Points $G,J,K,H$ are concyclic,
Circles $(EILF)$ and $(GJKH)$ are concentric.
Hint
Think of the Power of a Point theorem and the properties of inscribed angles.
Solution
3. Perpendicular bisectors of segments $EI$ and $LF$ meet at the center $M$ of $(EILF).$ On the other hand, $AM$ and $CM$ are the bisectors of angles $EAI$ ($=\angle EAF$) and $LCF$ ($=\angle ECF$), meaning that both pass through the midpoint of the arc $EF$ of $(EILF).$ Thus $M$ is the midpoint of that arc.
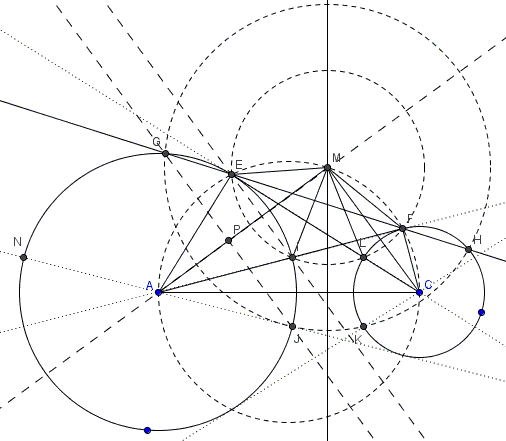
In passing, since $AC$ is a diameter of $(AEFC),$ $\angle AMC=90^{\circ}$ so that, $CM\parallel EI$ and $AM\parallel LF.$
4.The tangent at the midpoint of an arc is parallel to the chord that subtends that arc.
7. Let $AO\perp EG,$ $O$ the point of intersection. Since $\Delta AEG$ is isosceles, $AO$ bisects $EG$ and $\angle EAG.$
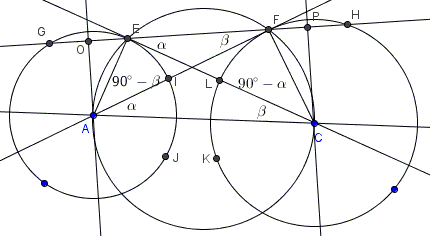
In circle $(AEFC)$ inscribed angles $CAF$ and $CEF$ are equal, say,
$CAF=CEF=\alpha.$
Similarly define
$ACE=AFE=\beta.$
Now, triangles $AFO$ and $ACE$ are right, so that
$\angle FAO=90^{\circ}-\beta=\angle CAE.$
Removing the common part ($\angle FAE$) we see that $\angle EAO=\angle CAF=\alpha.$ It follows that the central angles $EAG$ and $IAJ$ are also equal, implying $GE=IJ.$ $FH$ and $LK$ are treated similarly.
9. In part 7 we saw that, in circle $(A)$ two chords - $GE$ and $IJ$ - are equal. This makes the inscribed quadrilateral $EIJG$ a trapezoid with $EI\parallel GJ.$ But $EI,$ $GJ,$ and $CM$ are perpendicular to $AC$ such that all three are parallel.
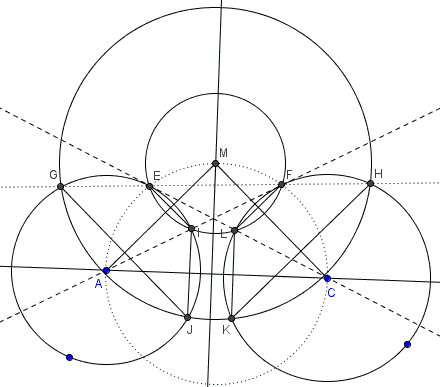
10-11. Points $E,I,L,F$ lie on circle $(M)=(EILF)$ centered at $M$ so that all four are equidistant from $M.$ Further, $AM$ is the perpendicular bisector of $EL$ and, since $EIJG$ is an isosceles trapezoid, it also bisects and is perpendicular to $GJ,$ making points $G$ and $J$ equididtsan from $M.$ Similarly, $MK=MH.$
Finally, $I$ and $L$ are equidistant from $M$ and $IL\parallel AC\parallel JK.$ it follows that the perpendicular bisector of $IL$ that passes through $M$ is also the perpendicular bisector of $JK,$ making $J$ and $K$ equidistant from $M.$ Thus, $MG=MJ=MK=MH.$
Acknowledgment
The above has been inspired by a post by Emmanuel Antonio José García at the CutTheKnotMath facebook page.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73595587
