Powers and Fractions Inequality
Problem
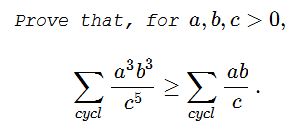
Proof 1
By the AM-GM inequality,
$\displaystyle\begin{align} \frac{a^3c^3}{b^5}+\frac{ba}{c}+\frac{cb}{a} &\ge 3\left(\frac{a^3c^3}{b^5}\cdot\frac{ba}{c}\cdot\frac{cb}{a}\right)^{1/3}\\ &=\frac{3ac}{b}. \end{align}$
Similarly, $\displaystyle\frac{b^3a^3}{c^5}+\frac{ac}{b}+\frac{cb}{a} \ge\frac{3ba}{c}\;$ and $\displaystyle\frac{c^3b^3}{a^5}+\frac{ac}{b}+\frac{ba}{c} \ge\frac{3cb}{a}.\;$ Adding up,
$\displaystyle\sum_{cycl}\frac{a^3c^3}{b^5}+2\sum_{cycl}\frac{ba}{c}\ge 3\sum_{cycl}\frac{ba}{c},$
which directly proves the required inequality.
Proof 2
By the AM-GM inequality,
$\displaystyle\begin{align} 2\sum_{cycl}\frac{a^3c^3}{b^5}&=\left(\frac{a^3c^3}{b^5}+\frac{b^3a^3}{c^5}\right)+\left(\frac{b^3a^3}{c^5}+\frac{c^3b^3}{a^5}\right)+\left(\frac{c^3b^3}{a^5}+\frac{a^3c^3}{b^5}\right)\\ &\ge 2\frac{a^3}{bc}+2\frac{b^3}{ca}+2\frac{c^3}{ab}\\ &= \left(\frac{a^3}{bc}+\frac{b^3}{ca}\right)+\left(\frac{b^3}{ca}+\frac{c^3}{ab}\right)+\left(\frac{c^3}{ab}+\frac{a^3}{bc}\right)\\ &\ge 2\frac{ab}{c}+2\frac{bc}{a}+2\frac{ca}{b}\\ &=2\sum_{cycl}\frac{ac}{b}. \end{align}$
Proof 3
The given inequality is equivalent to $\displaystyle\sum_{cycl}a^8b^8\ge a^4b^4c^4\sum_{cycl}a^2b^2.$
Let $a^2b^2=x,\;$ $b^2c^2=y,\;$ $c^2a^2=z,\;$ $x,y,z\gt 0.\;$ We need to prove that
(1)
$x^4+y^4+z^4\ge xyz(x+y+z).$
Schur's inequality for $t=2\;$ gives
(a)
$x^4+y^4+z^4+xyz(x+y+z)\ge xy(x^2+y^2)+yz(y^2+z^2)+zx(z^2+x^2).$
Now, $x^2+y^2\ge 2xy,\;$ etc., so that
(2)
$xy(x^2+y^2)+yz(y^2+z^2)+zx(z^2+x^2)\ge 2(x^2y^2+y^2z^2+z^2x^2).$
Further,
$\begin{align} 2(x^2y^2+y^2z^2+z^2x^2)&-2xyz(x+y+z)\\&=(xy-yz)^2+(yz-zx)^2+(zx-xy)^2\ge 0, \end{align}$
implying
(3)
$2(x^2y^2+y^2z^2+z^2x^2)\ge 2xyz(x+y+z).$
(2) and (3) give
(b)
$xy(x^2+y^2)+yz(y^2+z^2)+zx(z^2+x^2)\ge 2xyz(x+y+z).$
(a) and (b) add up to the required (1).
Proof 4
$\displaystyle\begin{align} 4\sum_{cycl}\frac{a^3b^3}{c^5} &= \sum_{cycl}\left(2\frac{a^3b^3}{c^5} + \frac{b^3c^3}{a^5} + \frac{c^3a^3}{b^5}\right)\\ &\ge \sum_{cycl}4\left(\frac{a^3b^3}{c^5}\cdot\frac{a^3b^3}{c^5}\cdot \frac{b^3c^3}{a^5}\cdot \frac{c^3a^3}{b^5}\right)^{1/4}\\ &= 4\sum_{cycl}\frac{ab}{c}. \end{align}$
Proof 5
As in Proof 3, the required inequality is reduced to
$\displaystyle\sum_{cycl}a^8b^8\ge a^4b^4c^4\sum_{cycl}a^2b^2.$
$\displaystyle 3\sum_{cycl}a^8b^8\ge \sum_{cycl}a^6b^6\sum_{cycl}a^2b^2.$
But, by the AM-GM inequality,
$\displaystyle \sum_{cycl}a^6b^6\ge 3\left(a^{12}b^{12}c^{12}\right)^{1/3}=3a^4b^4c^4.$
Acknowledgment
Dan Sitaru has kindly posted the above problem at the CutTheKnotMath facebook page, along with several solutions. The problem comes from his book Math Accent.
Proof 1 is by Ravi Prakash; Proof 2 is by Lâm Phan; Proof 3 is by Soumava Chakraborty; Proof 4 is by Rory Tarnow-Mordi.
- Schur's Inequality $(x^t(x-y)(x-z)+y^t(y-z)(y-x)+z^t(z-x)(z-y)\ge 0)$
- An Application of Schur's Inequality $\small{\left(5\left(\sum\sqrt{x+y}\right)\left(\sum\sqrt{(x+y)(y+z)}\right)\ge\left(\sum\sqrt{x+y}\right)^3+18\sqrt{(x+y)(y+z)(z+x)}\right)}$
- Powers and Fractions Inequality
- Three Junior Problems from Vietnam $\left(\left(\begin{array}{ccc}0&y&z\\x&0&z\\x&y&0\end{array}\right)\left(\begin{array}\;a\\b\\c\end{array}\right)=\left(\begin{array}\;x\\y\\z\end{array}\right)\right)$
- Newton's and Maclaurin's Inequalities $\left(E_k(X)\right)^2\gt E_{k-1}(X)E_{k+1}(X),$ $\left(\left(E_k(X)\right)^2\gt E_{k-1}(X)E_{k+1}(X)\right)$
- Rearrangement Inequality $\left(\displaystyle\sum_{i=1}^{n}x_iy_{n+1-i}\le\sum_{i=1}^{n}x_iy_{\sigma(i)}\le\sum_{i=1}^{n}x_iy_i\right)$
- Chebyshev Inequality $\left(\displaystyle n\sum_{i=1}^{n}x_iy_{i}\ge\sum_{i=1}^{n}x_i\sum_{i=1}^{n}y_i\right)$
- Chebyshev Holds a Key $\left(\displaystyle\sum_{k=1}^n\left[\left(\sum_{i=1}^k\sin a_i\right)\left(\sum_{i=1}^k\cos a_i\right)\right]\le\frac{n(n+1)(2n+1)}{12}\right)$
- Jensen's Inequality $\left( f(\lambda x_1+(1-\lambda )x_2)\le \lambda f(x_1)+(1-\lambda )f(x_2)\right)$
- Muirhead's Inequality $\left(\mathbf{a}\succ\mathbf{b}\;\right)$ implies $\left([\mathbf{a}]\ge [\mathbf{b}]\right)$
- Bergström's inequality $\left(\displaystyle \frac{x_1^2}{a_1}+\frac{x_2^2}{a_2}+\cdots+\frac{x_n^2}{a_n}\ge\frac{(x_1+x_2+\cdots+x_n)^2}{a_1+a_2+\cdots+a_n}\right)$
- Dorin Marghidanu's Example II $\left(\displaystyle \sum_{k=1}^n\frac{a^2_k}{a_{\sigma(k)}-1}\ge 4n\right)$
- Radon's Inequality and Applications $\left(\displaystyle \frac{x_1^{p+1}}{a_1^p}+\frac{x_2^{p+1}}{a_2^p}+\cdots+\frac{x_n^{p+1}}{a_n^p}\ge\frac{(x_1+x_2+\cdots+x_n)^{p+1}}{(a_1+a_2+\cdots+a_n)^p}\right)$
- Dorin Marghidanu's Example for Radon's Inequality $\left(\displaystyle\frac{a^{m+n+1}}{b^mc^n}+\frac{b^{m+n+1}}{c^ma^n}+\frac{c^{m+n+1}}{a^mb^n}\ge a+b+c\right)$
- Jordan and Kober Inequalities, PWW $\left(\displaystyle x\in\left(0,\frac{\pi}{2}\right)\,\Longrightarrow\,\sin x\gt\frac{2x}{\pi}\right)$
- A Mathematical Rabbit out of an Algebraic Hat $\left(x^{2} + y^{2} + z^{2} - xy - yz - zx \ge 0\right)$
- An Inequality With an Infinite Series $\left(\displaystyle \sum_{n=1}^{1000}\frac{1}{n^{3}+3n^{2}+2n} \lt \frac{1}{4}\right)$
- An Inequality: $\left(1/2 \cdot 3/4 \cdot 5/6 \cdot \ldots \cdot 99/100 \lt 1/10\right)$
- $\left(\text{A Low Bound for }1/2 \cdot 3/4 \cdot 5/6 \cdot \ldots \cdot (2n-1)/2n\right)$
- An Inequality: Easier to prove a subtler inequality
- Inequality with Logarithms (logπ3 + log3π > 2)
- An inequality: 1 + 1/4 + 1/9 + ... less than 2
- Inequality with Harmonic Differences $\left(\displaystyle\frac{2n}{3n+1} \lt \frac{1}{n+1}+\frac{1}{n+2}+\ldots +\frac{1}{n+n}\lt \frac{25}{36}\right)$
- An Inequality by Uncommon Induction $\left(\displaystyle 1+\frac{1}{2^2}+\frac{1}{3^2}+\ldots +\frac{1}{n^2}\gt \frac{3n}{2n+1}\right)$
- Hlawka's Inequality $\left(|x+y|+|y+z|+|z+x|\le |x|+|y|+|z|+|x+y+z|\right)$
- An Application of Hlawka's Inequality $\left(\sqrt{a^2-ab+b^2}+\sqrt{b^2-bc+c^2}+\sqrt{c^2-ca+a^2}\le a+b+c+\sqrt{a^2+b^2+c^2-ab-bc-ca}\right)$
- An Application of Hlawka's Inequality II $\left(\displaystyle xPA+yPB+zPC+\frac{a\sqrt{3}}{2}PM\ge (y+z)PA'+(z+x)PB'+(x+y)PC'\right)$
- Geometric Proof of Hlawka's Inequality $\left(|\vec{a}|+|\vec{b}|+|\vec{c}|+|\vec{d}|\ge |\vec{a}+\vec{d}|+|\vec{b}+\vec{d}|+|\vec{c}+\vec{d}|\right)$
- Hlawka-like Dinca's Inequality $\left((x+y)^{\alpha}+(y+z)^{\alpha}+(z+x)^{\alpha}\le x^{\alpha}+y^{\alpha}+z^{\alpha}+(x+y+z)^{\alpha}\right)$
- Hlawka-like Inequality for Convex Functions $\left(g(x) + g(y) + g(z) + g(x + y + z) \ge g(x + y) + g(x + z) + g(y + z)\right)$
- Hlawka in Convex Quadrilateral $\left(AB+BC+CD+DA\gt AC+BD+2EF\right)$
- Quadrilateral Inequality
- Problem 4165 from Crux Mathematicorum $\left(\displaystyle \left|\sum_{i=1}^4x_i\right|+2\sum_{i=1}^4|x_i|\ge 6\sqrt[6]{\prod_{1\le i\lt j\le 4}|x_i+x_j|}\right)$
- An Inequality in Determinants $\left(\left|\begin{array}{ccc} 1 & 1 & 1\\ a & b & c\\ a^4 & b^4 & c^4\\ \end{array}\right|\ge \left|\begin{array}{ccc} 1 & 1 & 1\\ a & b & c\\ a^3 & b^3 & c^3. \end{array}\right|\right)$
- Application of Cauchy-Schwarz Inequality $\left(\displaystyle\sqrt{a^2-1}+\sqrt{b^2-1}+\sqrt{c^2-1}\le\frac{ab+bc+ca}{2}\right)$
- An Inequality from Tibet $\left((bcde+acde+abde+abce+abcd)^4\ge 125(a+b+c+d+e)(abcde)^3\right)$
- An Inequality from Morocco $\left(\displaystyle 4|(a-b)(b-c)(c-d)(d-a)|\le abcd\right)$
- An Inequality for Mixed Means $\small{\left(\displaystyle \sqrt[m]{\prod_{j=1}^{m}\left[a_j+\frac{1}{n}\sum_{i=1}^{n}x_i\right]}\ge\frac{1}{n}\sum_{i=1}^{n}\sqrt[m]{\prod_{j=1}^{m}(a_j+x_i)} \ge\prod_{i=1}^{n}\prod_{j=1}^{m}\sqrt[mn]{a_j+x_i}\right)}$
- An Inequality in Integers $\left(\displaystyle\frac{a}{b}+\frac{1}{ab}\lt\sqrt{7}\right)$
- An Inequality in Integers II $\left(\displaystyle\frac{a^3+b^3+c^3}{3}-abc\ge 3k\right)$
- An Inequality in Integers III $\left(\displaystyle\sum_{i,j=1}^n \frac{i^2j^2}{i+j-1}\gt n^3\right)$
- An Inequality with Exponents $\left(\displaystyle e^{\frac{4}{e}}\left(b\cdot a^{2\sqrt{a}}+c\cdot b^{2\sqrt{b}}+a\cdot c^{2\sqrt{c}}\right)\ge 3\sqrt[3]{abc}\right)$
- Exponential Inequalities for Means $\left(\displaystyle A_n^{G_nH_n}\le G_n^{A_nH_h}\le H_n^{A_nG_n}\right)$
- A Simple Inequality in Three Variables $\left(\displaystyle\sum_{cyc}ac\left(\frac{1}{2a+b}+\frac{1}{2c+b}\right)\le \sqrt{3(a^2+b^2+c^2)}\right)$
- An Asymmetric Inequality $\left((a+b)(a+c)\ge 2\sqrt{abc(a+b+c)}\right)$
- Linear Algebra Tools for Proving Inequalities $\left(\displaystyle\left(\frac{a}{b-c}\right)^2+\left(\frac{b}{c-a}\right)^2+\left(\frac{c}{a-b}\right)^2\ge 2.\right)$
- An Inequality with a Generic Proof $\left(2\sqrt{b}+\sqrt{aS+b}\le \sqrt{ax+b}+ \sqrt{ay+b}+ \sqrt{az+b}\le \sqrt{3aS+9b}\right)$
- A Generalization of an Inequality from a Romanian Olympiad $\left(\displaystyle \frac{2}{n-1}\sum_{1\le i\lt j\le n}a_{i}a_{j}\le\ln\left(\prod_{k=1}^{n}a_{k}^{a_{k}}\right)+\frac{1}{e}\sum_{k=1}^{n}e^{a_{k}}\right)$
- Area Inequality in Trapezoid $\left([PQRS]\le\frac{1}{4}[ABCD]\right)$
- Improving an Inequality $\left(\displaystyle\sum_{k=1}^{n}\frac{1}{\sqrt{k}}\gt 2(\sqrt{n+1}-1)\right)$
- RomanoNorwegian Inequality $\left(\sqrt{\cot A} + \sqrt{\cot B} + \sqrt{\cot C} \ge 2\right)$
- Inequality with Nested Radicals II $\left(\displaystyle\sqrt{n+1}\le\sqrt{n+\sqrt{(n-1)+\sqrt{\ldots+\sqrt{2+\sqrt{1}}}}}\le\sqrt{2n-1}\right)$
- Inequality with Powers And Radicals $\left(\displaystyle\sum_{cycl}\sqrt[6]{ab^2c^3}\ge\sum_{cycl}\sqrt[30]{a^9b^{10}c^{11}}\right)$
- Inequality with Two Minima $\left(\displaystyle\sqrt{a-c}+\sqrt{b-c}\le\min \left\{\sqrt{\frac{ab}{c}},\sqrt{2(a+b-2c)} \right\}\right)$
- Simple Inequality with Many Faces And Variables $\left(\displaystyle \frac{a^2}{c-1}+\frac{b^2}{d-1}+\frac{c^2}{e-1}+\frac{d^2}{a-1}+\frac{e^2}{b-1}\ge 20\right)$
- An Inequality with Determinants $\left(\displaystyle\left|\begin{array}{cccc}\,a&-b&0&0\\0&b&-c&0\\0&0&c&-d\\1&1&1&1+d\end{array}\right|\ge 3\sqrt[3]{4}(abcd)^{5/6}\right)$
- An Inequality with Determinants II $\left(\displaystyle \Delta=\left|\begin{array}{cccc} \,1 & 1 & 1 & 1\\ a & b & c & d\\ a^2 & b^2 & c^2 & d^2\\ \frac{1}{a^2} & \frac{1}{b^2} & \frac{1}{c^2} & \frac{1}{d^2} \end{array}\right|\lt \frac{1}{abcd}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right)\right)$
- An Inequality with Determinants III $\left(\displaystyle \left|\begin{array}{ccccc} \,0 & x^2 & y^2 & z^2 & 1\\ x^2 & 0 & x^2+y^2 & x^2+z^2 & 1\\ y^2 & x^2+y^2 & 0 & y^2+z^2 & 1\\ z^2 & x^2+z^2 & y^2+z^2 & 0 & 1\\ 1 & 1 & 1 & 1 & 0\end{array}\right|\le \left|\begin{array}{ccccc} \,0 & a^2 & b^2 & c^2 & 1\\ a^2 & 0 & a^2+b^2 & a^2+c^2 & 1\\ b^2 & a^2+b^2 & 0 & b^2+c^2 & 1\\ c^2 & a^2+c^2 & b^2+c^2 & 0 & 1\\ 1 & 1 & 1 & 1 & 0\end{array}\right|\right)$
- An Inequality with Determinants IV $\left(\displaystyle\left|\begin{array}{cccc}\,a&-b&0&0\\0&b&-c&0\\0&0&c&-d\\1&1&1&1+d\end{array}\right|\ge 3\sqrt[3]{4}(abcd)^{5/6}\right)$
- An Inequality with Determinants V $\left(\displaystyle \Delta =\left|\begin{array}{cccc} \,s & \frac{a^2b}{a^3+b} & \frac{b^2c}{b^3+c} & \frac{c^2a}{c^3+a}\\ \frac{a^2b}{a^3+b} & s & \frac{c^2a}{c^3+a} & \frac{b^2c}{b^3+c}\\ \frac{b^2c}{b^3+c} & \frac{c^2a}{c^3+a} & s & \frac{a^2b}{a^3+b}\\ \frac{c^2a}{c^3+a} & \frac{b^2c}{b^3+c} & \frac{a^2b}{a^3+b} & s\end{array}\right|\ge 0\right)$
- An Inequality with Determinants VI $\left(\displaystyle\frac{\Delta_1-\Delta_2}{(b-a)(a-c)(b-c)}\ge 12\sqrt[6]{(abc)^5}\right)$
- An Inequality with Determinants VII $\left(\displaystyle \left|\begin{array}{ccccc} \,0 & a^2 & b^2 & c^2 & 1\\ a^2 & 0 & a^2+b^2 & a^2+c^2 & 1\\ b^2 & a^2+b^2 & 0 & b^2+c^2 & 1\\ c^2 & a^2+c^2 & b^2+c^2 & 0 & 1\\ 1 & 1 & 1 & 1 & 0\end{array}\right| \le\frac{1}{8}\prod_{cycl}(a+b)^2\right)$
- An Inequality in Reciprocals $\left(\displaystyle\begin{align}\frac{4}{9}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)&+4\left(\frac{1}{a+2b}+\frac{1}{b+2c}+\frac{1}{c+2a}\right)\\ &\ge 5\left(\frac{1}{2a+b}+\frac{1}{2b+c}+\frac{1}{2c+a}\right)+\frac{1}{a+b+c}. \end{align}\right)$
- An Inequality in Reciprocals II $\left(\displaystyle \frac{1}{4a+1} + \frac{1}{4b+1} + \frac{6}{2a+2b+1} \ge \frac{4}{3a+b+1} + \frac{4}{3b+a+1}\right)$
- An Inequality in Reciprocals III $\left(\displaystyle \frac{1}{3}\sum_{cycl}\frac{1}{a+b} + \sum_{cycl}\frac{1}{4a+b+c}\ge\sum_{cycl}\left(\frac{1}{a+2b+3c}+\frac{1}{a+3b+2c}\right)\right)$
- A Problem from the Danubius Contest 2016 $\left(\displaystyle\{E(a,b)|\;a\gt 0, b\gt 0\}\subset \left(\frac{11}{10},\frac{10}{9}\right]\right)$
- A Problem from the Danubius-XI Contest $\left(\displaystyle\frac{a+b}{(1+c)^2}+\frac{b+c}{(1+a)^2}+\frac{c+a}{(1+b)^2}\ge\frac{9S}{(9+S)^2}\right)$
- An Inequality with Integrals and Rearrangement $\left(\displaystyle \sum_{cycl}b^2c^3\int_0^a(\cot x)(\arctan x)dx\lt abc(a^3+b^3+c^3)\right)$
- An Inequality with Cot, Cos, and Sin $\left(\displaystyle\sum_{cycl}\cot^2A\,\cot^2B\ge\frac{\displaystyle\sum_{cycl}\cos^2A}{\displaystyle\sum_{cycl}\sin^2A}\right)$
- A Trigonometric Inequality from the RMM $\left(\displaystyle\sin (x+y)\le\sin x\left(\frac{\sin y}{y}\right)^3+\sin y\left(\frac{\sin x}{x}\right)^3\right)$
- An Inequality with Finite Sums $\left(\displaystyle\sum_{k=1}^n\frac{(2+x)^k}{2+x\cdot k}\ge 2^n-1\right)$
- Hung Viet's Inequality $\left(\displaystyle 1+\sum_{cycl}\frac{ab}{a^2-ab+b^2}\ge\frac{3}{2}\cdot\frac{(a+b)(b+c)(c+a)}{a^3+b^3+c^3}\right)$
- Hung Viet's Inequality II $\left(\displaystyle\min_{all}(a-b)^2\le\frac{a^2+b^2+c^2+d^2}{5}\right)$
- Hung Viet's Inequality III $\left(\displaystyle \left(\sum_{cycl}a^4\right)\left(\sum_{cycl}ab^3\right)\ge\left(\sum_{cycl}a^3b\right)\left(\sum_{cycl}a^2b^2\right)\right)$
- Inequality by Calculus $\left(\displaystyle\frac{b^{n+1}-a^{n+1}}{n+1}+\frac{ab(b^{n-1}-a^{n-1})}{n-1}\leq (b-a)\sqrt{2(a^{2n}+b^{2n})}\right)$
- Dorin Marghidanu's Calculus Lemma
$\left(\displaystyle u^v\gt\frac{u}{u+v}\right)$
- An Inequality with Exponents from a Calculus Lemma $\left(\displaystyle a^b\cdot (a+b)^c\cdot (a+b+c)^d\gt\frac{a}{a+b+c+d}\right)$
- An Inequality with Exponents from a Calculus Lemma II $\left(2^a(b+c)^{1-a}+2^b(c+a)^{1-b}+2^c(a+b)^{1-c}\lt 4(a+b+c)\right)$
- An Area Inequality $\left(\displaystyle a^{2} + b^{2} + u^{2} + v^{2} + au + bv \ge \frac{3}{2}\right)$
- A 4-variable Inequality from the RMM $\left(\displaystyle |(a-b)(b-c)(c-a)|\le\sum_{cycl}|a-b||a+c+\eta||b+c+\eta|\right)$
- An Inequality from RMM with Powers of 2 $\left(2^x+2^y+2^z+2^{x+y+z}\gt\sqrt[x+y]{16^{xy}}+\sqrt[y+z]{16^{yz}}+\sqrt[z+x]{16^{zx}}+1\right)$
- A Cycling Inequality with Integrals $\bigg(2bc\Omega(a)+2ca\Omega(b)+2ab\Omega(c)\lt a^2+b^2+c^2$ where $\Omega(t)=\displaystyle\int_{0}^{1}\frac{1-x^2}{1+tx^2+x^4}dx\bigg)$
- A Cycling Inequality with Integrals II $\bigg(\Omega(a,b,c)+\Omega(b,c,a)+\Omega(c,a,b)\le 1,$ where $\Omega(p,q,r)=\displaystyle\int_{0}^{1}\frac{x^p}{1+x^p+x^{q+r}}dx\bigg)$
- An Inequality with Absolute Values $\left(\displaystyle\sum_{cycl}\frac{|a|+|b|}{1-c^2} \ge \sum_{cycl}\frac{2|a|}{1-bc}\right)$
- An Inequality from RMM with a Generic 5 $\left(\displaystyle\sqrt[3]{(2a+5)(2b+5)(2c+5)}\ge\frac{6abc}{ab+bc+ca}+5\right)$
- An Elementary Inequality by Non-elementary Means $\left(12(a\sin a + \cos a - 1)^2 \le 2a^4 + a^3\sin 2a\right)$
- Inequality in Quadrilateral $\left(\displaystyle\sum_{cycl}\sqrt{a^2+b^2+c^2}\gt 2\sqrt{3\cdot AC\cdot BD}\right)$
- Marian Dinca's Refinement of Nesbitt's Inequality $\left(\displaystyle\begin{align}\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}&\ge\frac{(a+b+c)^2}{2(ab+bc+ca)}\\&\ge\frac{3\sqrt{3(a^2+b^2+c^2)}}{2(a+b+c)}\\&\ge\frac{3}{2}\end{align}\right)$
- An Inequality in Cyclic Quadrilateral $\left(\displaystyle\frac{R}{8\sqrt{2}}\ge\frac{\sqrt[4]{(abcd)^3}}{(a+b+c+d)^2}\right)$
- An Inequality in Cyclic Quadrilateral II $\left(\displaystyle\sin A\sin B\le (\frac{s}{a}-1)(\frac{s}{b}-1)(\frac{s}{c}-1)(\frac{s}{d}-1)\right)$
- An Inequality in Cyclic Quadrilateral III $\left(\displaystyle\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2}\cos\frac{D}{2}\le\frac{S^2}{4abcd}\right)$
- An Inequality in Cyclic Quadrilateral IV $\left(a^2-b^2-c^2+d^2+4S\le 2\sqrt{2}(ad+bc)\right)$
- Inequality with Three Linear Constraints $\left(\displaystyle\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge 1\right)$
- Inequality with Three Numbers, Not All Zero $\left(\displaystyle\frac{a^2-ab+b^2}{b^2+bc+c^2}+\frac{b^2-bc+c^2}{c^2+ca+a^2}+\frac{c^2-ca+a^2}{a^2+ab+b^2}\ge 1\right)$
- An Easy Inequality with Three Integrals $\left(\displaystyle a^2\int_{0}^{b}\frac{\arctan x}{x}dx + b^2\int_{0}^{c}\frac{\arctan x}{x}dx + c^2\int_{0}^{a}\frac{\arctan x}{x}dx \lt a^3+b^3+c^3\right)$
- Divide And Conquer in Cyclic Sums $\left(\displaystyle \sum_{cycl}c\left(\frac{4a}{b^2}+\frac{3b}{a^2}\right)\ge 12+3\sum_{cycl}\frac{a}{b}\right)$
- Wu's Inequality $\left((x^2+xy+y^2)(y^2+yz+z^2)(z^2+zx+x^2)\ge (xy+yz+zx)^3\right)$
- Dorin Marghidanu's Inequality in Complex Plane $\left(\displaystyle \sum_{cycl}(|(2-n)\cdot z_1+z_2+\ldots+z_n|\ge\sum_{k=1}^n|z_k|\right)$
- Dorin Marghidanu's Inequality in Integer Variables $\left(\displaystyle \frac{m}{\sqrt[m]{1+n}}+\frac{n}{\sqrt[n]{1+m}}\gt\frac{m+n}{2}\right)$
- Dorin Marghidanu's Inequality in Many Variables $\left(\displaystyle\prod_{k=1}^{n}\sqrt[n]{\frac{\displaystyle \sum_{i=1,i\ne k}^{k}a_i}{a_k)}} \ge n-1\right)$
- Dorin Marghidanu's Inequality in Many Variables Plus Two More $\left(\displaystyle G_n\left[p+\frac{r}{a_1},p+\frac{r}{a_2},\ldots,p+\frac{r}{a_n}\right]\ge p+\frac{r}{A_n[a_1,a_2,\ldots,a_n]}\right)$
- Dorin Marghidanu's Inequality with Radicals $\left(\displaystyle\sum_{k=1}^{n}\sqrt[i_k]{x_k} \gt \sqrt[\small{\displaystyle \sum_{k=1}^{n}i_k}]{\prod_{k=1}^{n}x_k}\right)$
- Dorin Marghidanu's Light Elegance in Four Variables $\left(\displaystyle \sum_{cycl}(-a+b+c+d)^2\ge 2(a+b+c+d)-1\right)$
- Dorin Marghidanu's Spanish Problem $\left(\displaystyle n^*\le (n_*)^2\right)$
- Two-Sided Inequality - One Provenance $\left(\displaystyle\sum_{k=1}^{2n(n+1)}\frac{1}{\sqrt{2k}+\sqrt{2k+1}}\lt n\lt\sum_{k=1}^{2n(n+1)}\frac{1}{\sqrt{2k-1}+\sqrt{2k}}\right)$
- An Inequality with Factorial $\left(a_1\cdot a_2\cdot\ldots\cdot a_n+(1-a_1)\cdot (2-a_2)\cdot\ldots\cdot (n-a_n)\le n!\right)$
- Wonderful Inequality on Unit Circle $\left(\displaystyle\left(\frac{a+b}{1+ab}\right)^2+\left(\frac{a-b}{1-ab}\right)^2\ge 1\right)$
- Quadratic Function for Solving Inequalities $\left((a^2+3x^2)(b^2+3y^2)(c^2+3z^2)\ge 4(ayz+bzx+cxy+xyz)^2\right)$
- An Inequality Where One Term Is More Equal Than Others $\left(\displaystyle\left(\sum_{k=1}^na_k\right)\left(\sum_{k=1}^n\frac{1}{a_k}\right)\ge n^2+(n-2)^2\right)$
- Complicated Constraint - Simple Inequality $\left(3(a+b)(b+c)(c+a)\ge\frac{\displaystyle 8}{\displaystyle\sqrt[8]{a^3+b^3+c^3}}\right)$
- The power of substitution II: proving an inequality with three variables $\left(\displaystyle\frac{ab}{(a+b)^2}+\frac{bc}{(b+c)^2}+\frac{ca}{(c+a)^2}\le\frac{1}{4}+\frac{4abc}{(a+b)(b+c)(c+a)}\right)$
- Algebraic-Geometric Inequality $\left(\sqrt{x^2-\sqrt{3}xy+y^2} + \sqrt{y^2-\sqrt{2}yz+z^2} \ge \sqrt{z^2-zx+x^2}\right)$
- One Inequality - Two Domains $\left(\displaystyle 3\prod_{cycl}(a^2+ab+b^2)\ge\left(\sum_{cycl}a\right)^2\cdot\left(\sum_{cycl}ab\right)^2\right)$
- Radicals, Radicals, And More Radicals in an Inequality $\bigg(\displaystyle\gamma=\frac{\sqrt[4]{xz}}{\sqrt{x}+\sqrt{z}}.\,$ Prove that $\sqrt{x}+\sqrt{y}+\sqrt{z}\ge 2\gamma\sqrt{3(x+y+z)}\bigg)$
- An Inequality in Triangle and In General $\left(\displaystyle\sum_{cycl}\frac{\cot A\,\cot^3B}{\cot^2B+2\cot^2A}+2\sum_{cycl}\frac{\cot^2A\cot B}{\cot A+2\cot B}\ge 1\right)$
- Dan Sitaru's Cyclic Inequality In Many Variables $\left(\displaystyle a+b+c+d\le \frac{a^5+b^5+c^5+d^5}{abcd}\right)$
- An Inequality on Circumscribed Quadrilateral $\left(s\ge 4R\right)$
- An Inequality with Fractions $\left(\displaystyle m\le\frac{a_1+a_2+\ldots+a_n}{b_1+b_2+\ldots+b_n}\le M\right)$
- An Inequality with Complex Numbers of Unit Length $\left(|a-b|+|a-c|\ge |a+b|+|a+c|\right)$
- An Inequality with Complex Numbers of Unit Length II $\left(|a^2+bc|\ge |b+c|\right)$
- Le Khanh Sy's Problem $\left(xa^2+yb^2+zc^2\ge 2m\right)$
- An Inequality Not in Triangle $\left(\displaystyle\sqrt{a^2+b^2-ab\sqrt{2}}+\sqrt{b^2+c^2-bc\sqrt{3}}+\sqrt{c^2+d^2-\frac{cd(\sqrt{6}+\sqrt{2})}{2}}\ge\sqrt{a^2+d^2}\right)$
- An Acyclic Inequality in Three Variables $\left(\displaystyle \frac{(a^2-bc)^2+(b^2-ca)^2+(c^2-ab)^2}{a^2+b^2+c^2+ab+bc+ca}\geq 3(a-b)(b-c)\right)$
- An Inequality with Areas, Norms, and Complex Numbers $\left(\displaystyle \frac{(ad-bc)(3(a^2+b^2)(c^2+d^2)-4(ad-bc)^2)}{\left((a^2+b^2)(c^2+d^2)\right)^{\frac{3}{2}}}\le 1\right)$
- Darij Grinberg's Inequality In Three Variables $\left(a^2+b^2+c^2+2abc+1\ge 2(ab+bc+ca)\right)$
- Small Change Makes Big Difference $\left(\displaystyle\frac{1}{\displaystyle \sqrt{1+a^2-\frac{(a-b)^2}{2}}}+\frac{1}{\displaystyle \sqrt{1+b^2-\frac{(a-b)^2}{2}}}\ge\frac{2}{\sqrt{1+ab}}\right)$
- Inequality with Two Variables? Think Again $\left(\displaystyle\frac{1}{\sqrt{1+a^2}}+\frac{1}{\sqrt{1+b^2}}\le\frac{2}{\sqrt{1+ab}}\right)$
- A Problem From a Mongolian Olympiad for Grade 11 $\left(\displaystyle \frac{a}{3a+2b^3}+ \frac{b}{3b+2c^3}+ \frac{c}{3c+2a^3}\le\frac{1}{5}\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\right)$
- Sitaru--Schweitzer Inequality
$\left(\displaystyle \left(\int_{a}^{b}f(x)dx\right)\left(\int_{a}^{b}\frac{1}{f(x)}dx\right)\le\frac{(m+M)^2}{4mM}(b-a)^2\right)$
- Pólya-Szegö Inequality $\left(\displaystyle \frac{\displaystyle \left(\sum_{k=1}^{n}a^2_{k}\right)\left(\sum_{k=1}^{n}b^2_{k}\right)}{\displaystyle\left(\sum_{k=1}^{n}a_{k}b_{k}\right)^2}\le\left(\frac{\displaystyle \sqrt{\frac{M_1M_2}{m_1m_2}}+\sqrt{\frac{m_1m_2}{M_1M_2}}}{2}\right)^2\right)$
- Kantorovich Inequality $\left(\displaystyle \left(\sum_{k=1}^{n}\gamma_ku_k^2\right)\left(\sum_{k=1}^{n}\frac{1}{\gamma_k}u_k^2\right)\le\frac{1}{4}\left(\sqrt{\frac{M}{m}}+\sqrt{\frac{m}{M}}\right)^2\left(\sum_{k=1}^{n}u^2_{k}\right)^2\right)$
- Greub-Rheinboldt Inequality $\left(\displaystyle \left(\sum_{k=1}^{n}a_k^2u_k^2\right)\left(\sum_{k=1}^{n}b_k^2u_k^2\right)\le\frac{(M_1M_2+m_1m_2)^2}{4m_1m_2M_1M_2}\left(\sum_{k=1}^{n}a_kb_ku^2_{k}\right)^2\right)$
- An Inequality with Cyclic Sums And Products $\left(\small{\displaystyle \sum_{cycl}\frac{a^2}{(b+c+d+e)(a-b)(a-c)(a-d)(a-e)}\lt\frac{(a+b+c+d+e)^2}{1024abcde}}\right)$
- Problem 1 From the 2016 Pan-African Math Olympiad $\left(\displaystyle \sum_{cycl}\frac{1}{(x+1)^2+y^2+1}\le\frac{1}{2}\right)$
- An Inequality with Integrals and Radicals $\left(\displaystyle \Bigr(\int_0^1 \sqrt[3]{f(x)}dx\Bigr)\Bigr(\int_0^1 \sqrt[5]{f(x)}dx\Bigr)\Bigr(\int_0^1 \sqrt[7]{f(x)}dx\Bigr)\leq 1\right)$
- Twin Inequalities in Four Variables: Twin 1 $\left(\displaystyle (ac+bd)^2\le\left(b\sqrt[5]{ab^4}+d\sqrt[5]{cd^4}\right)\left(a\sqrt[5]{a^4b}+c\sqrt[5]{c^4d}\right)\right)$
- Twin Inequalities in Four Variables: Twin 2 $\left(\displaystyle (a\sqrt[3]{a^2b}+c\sqrt[3]{c^2d})(b\sqrt[3]{ab^2}+d\sqrt[3]{cd^2})\le (a^2+c^2)(b^2+d^2)\right)$
- Simple Inequality with a Variety of Solutions $\left(\displaystyle \sum_{cycl}\left(\frac{\ln x}{\ln y\ln z}+\frac{\ln y}{\ln z\ln x}\right)\ge\frac{18}{\ln (xyz)}\right)$
- A Partly Cyclic Inequality in Four Variables $\left(\displaystyle \sum_{cycl}xe^x\ge (x+y+2)e^{x+y+2}+(z+t-2)\sqrt[3]{e^{z+t-2}}\right)$
- Dan Sitaru's Inequality by Induction $\left(\displaystyle\begin{align}&\small{\frac{3}{a+1}+\frac{3}{b+1}+\frac{2}{c+1}+\frac{1}{d+1}}\\ &\small{\qquad\le 6+\frac{1}{a+b+1}+\frac{1}{a+b+c+1}+\frac{1}{a+b+c+d+1}}\end{align}\right)$
- An Inequality in Three (Or Is It Two) Variables $\left(\displaystyle \frac{(x+y)^2}{(x\sin^2z+y\cos^2z)(x\cos^2z+y\sin^2z)}+\frac{x}{y}+\frac{y}{x}\geq 6\right)$
- An Inequality in Four Weighted Variables $\left(\displaystyle (a+c)^c(b+d)^d(c+d)^{c+d}\le c^cd^d(a+b+c+d)^{c+d}\right)$
- An Inequality in Fractions with Absolute Values $\left(\displaystyle \omega\lt\frac{1}{3}\left(\sum_{cycl}\frac{a|a|-b|b|}{a-b}\right)\lt 2\Omega\right)$
- Inequalities with Double And Triple Integrals $\left(\displaystyle \int_0^{\frac{\pi}{2}}\int_0^{\frac{\pi}{2}}\cos\left(\frac{x+y}{2}\right)dxdy\ge\frac{\pi}{2}\right)$
- An Old Inequality $\left(\displaystyle \frac{4ab}{(a+b)^2}\ge\cos\left(\frac{\pi}{2}\cdot\frac{a-b}{a+b}\right)\right)$
- Dan Sitaru's Amazing, Never Ending Inequality $\left(\displaystyle \small{\sum_{cycl}\left(\frac{a}{b}\right)^2\cdot\sum_{cycl}\left(\frac{a}{b}\right)^4\cdot\sum_{cycl}\left(\frac{a}{b}\right)^8\ge\sum_{cycl}\left(\frac{a}{c}\right)\cdot\sum_{cycl}\left(\frac{b}{a}\right)\cdot\sum_{cycl}\left(\frac{b}{c}\right)}\right)$
- Leo Giugiuc's Exercise $\left(\displaystyle x\sin x+x^2\cos x\le 2\sin^2x\right)$
- Another Inequality with Logarithms, But Not Really $\left(\displaystyle \sum_{cycl}\frac{\log_y^3x+\log_z^3y}{\log_y^2x+\log_zx+\log_z^2y}\geq 2\right)$
- An Inequality Solved by Changing Appearances $\left(\displaystyle \sum_{cycl}a^2\cdot\sum_{cycl}\frac{1}{x^2}+\frac{\displaystyle 2\sum_{cycl}ab\cdot\sum_{cycl}x}{xyz}\ge 0\right)$
- Distances to Three Points on a Circle $\left(3\le |z-a|+|z-b|+|z-c|\le 4\right)$
- An Inequality with Powers And Logarithm $\left(\displaystyle \frac{a}{b}+\frac{a^2}{b^2}+\frac{a^3}{b^3}+12\ln b\ge\frac{b}{a}+\frac{b^2}{a^2}+\frac{b^3}{a^3}+12\ln a\right)$
- Four Integrals in One Inequality $\left(\displaystyle \small{\left(\int_a^bxf(x)dx\right)\left(\int_a^bf^2(x)dx\right)\left(\int_a^bx^3f(x)dx\right)\ge\frac{a^2b^2}{b-a}\left(\int_a^bf(x)dx\right)^4}\right)$
- Same Integral, Three Intervals $\left(\displaystyle\small{I(u,v)=\int_u^v\left(\arctan\left(\frac{u\sin x}{v+u\cos x}\right)+\arctan\left(\frac{v\sin x}{u+v\cos x}\right)\right)dx}\right)$
- Dorin Marghidanu's Inequality with Generalization $\left(\displaystyle (x+y)^2+(y+z)^2+(z+x)^2+12ab\le 4(a+b)(x+y+z)\right)$
- Dan Sitaru's Inequality with Three Related Integrals and Derivatives $\left(\displaystyle\small{\left(\int_0^af(x)dx\right)^4\leq \frac{a^8}{60}\left(\int_0^a \left(f'(x)\right)^2 dx\right)\left(\int_0^a \left(f''(x)\right)^2dx\right)}\right)$
- An Inequality in Two Or More Variables $\left(\displaystyle \frac{a}{1+a}+\frac{b}{(1+a)(1+b)}+\frac{c}{(1+a)(1+b)(1+c)}\geq \frac{7}{8}\right)$
- An Inequality in Two Or More Variables II $\left(\displaystyle (a+1)^{a+1}\cdot (b+1)^{b+1}\cdot (c+1)^{c+1}\le e^{a+b+c}\cdot\sqrt{e^{a^2+b^2+c^2}}\right)$
- A Not Quite Cyclic Inequality $\left(\displaystyle \frac{a^2+b^2+c^2}{a+b+c} \le \frac{ab+bc+ca}{a+b+c} + |a-b|+|b-c|\right)$
- Dan Sitaru's Inequality: From Three Variables to Many in Two Ways $\left(\displaystyle a+b+c\ge\frac{3}{2}\right)$
- An Inequality with Sines But Not in a Triangle $\left(\displaystyle \prod_{cycl}\Bigr(a^2\sin \frac{2\pi}{a}+(a+1)^2\sin \frac{2\pi}{a+1}\Bigr)\gt 2^{16}\right)$
- An Inequality with Angles and Integers $\left(\displaystyle k^2\tan \alpha +l^2\tan \beta \geq \frac{2kl}{\sin (\alpha+\beta)}-(k^2+l^2)\cot (\alpha+\beta)\right)$
- Sladjan Stankovik's Inequality In Four Variables $\left(\displaystyle 2\sum_{cycl}a^2-3\frac{\displaystyle \sum_{cycl}a^3}{\displaystyle \sum_{cycl}a}\le\sum_{all}ab\right)$
- An Inequality with Two Pairs of Triplets $\left(\displaystyle (a^2+b^2+c^2)\left(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}\right)+\frac{2(ab+bc+ca)(x+y+z)}{xyz}\ge 0\right)$
- A Refinement of Turkevich's Inequality $\left(\displaystyle a^2+b^2+c^2+d^2+\frac{32abcd}{(a+b+c+d)^2}\ge \sum_{sym}ab\right)$
- Dan Sitaru's Exercise with Pi and Ln $\left(\displaystyle \small{\arctan(z-x)+\arctan(z-y)+\arctan(y-x) \lt \frac{\pi}{2} - \ln(2)}\right)$
- Leo Giugiuc's Cyclic Quickie in Four Variables $\left(3(xyz+yzt+ztx+txy)^2\ge 8(xy+xz+xt+yz+yz+zt)xyzt\right)$
- Dan Sitaru's Cyclic Inequality in Four Variables $\left(\displaystyle \sum_{cycl}\frac{a^7}{bcd+a^3}\ge 2abcd\right)$
- A Not Quite Cyclic Inequality from Tibet $\left((x+y)^2(z^2+xz+x^2+xy+y^2+yz)^2\ge 8(xy+yz+zx)^2(x^2+y^2)\right)$
- An inequality in 2+2 variables from SSMA magazine $\left(\displaystyle k^2\tan\alpha+l^2\tan\beta\ge\frac{2kl}{\sin (\alpha+\beta)}-(k^2+l^2)\cot(\alpha+\beta)\right)$
- Kunihiko Chikaya's Inequality with Parameter $\bigg(p \ge 2.$ Prove $\displaystyle \sum_{cycl}\frac{a}{\sqrt{ap+b}} \le \sqrt{\frac{3(a+b+c)}{p+1}}\bigg)$
- Dorin Marghidanu's Permuted Inequality $\left(\displaystyle \sum_{k=1}^n\left(a_k+\frac{1}{a_{\sigma(k)}}\right)^p\ge \frac{(s^2+n^2)^p}{n^{p-1}s^p}\right)$
- An Inequality Involving Arithmetic And Geometric Means $\left(\displaystyle\sum_{cycl}\frac{1}{a^4+b^4+c^4+abcd}\le \frac{1}{abcd}\right)$
- Dorin Marghidanu's Sums and Products $\left(\displaystyle \sum_{k=1}^n\frac{a_k}{P_kS_k}\ge\frac{n^n}{\displaystyle (n-1)S^{n-1}}\right)$
- Simple Nameless Inequality $\left(\displaystyle \sum_{k=1}^n\frac{S}{S_k}\ge\frac{n^2}{n-1}\right)$
- Volume Inequality in Tetrahedron $\left(OA\cdot OB\cdot OC\ge 27xyz\right)$
- Inequality in Convex Quadrilateral $\left(\displaystyle\frac{\displaystyle \sum_{cycl}\sqrt{b+c+d-a}}{a+b+c+d}\ge\sqrt{\frac{2(a+b+c+d)}{a^2+b^2+c^2+d^2}}\right)$
- Dan Sitaru's Inequality with a Double Integral $\left(\displaystyle\begin{align}&\small{\int_0^1\int_0^1\sqrt{\left(m^2\sqrt{mnf(x)f(y)}+f^2(x)\right)\left(n^2\sqrt{mnf(x)f(y)}+f^2(y)\right)}dxdy}\\ &\qquad\qquad\qquad\qquad\small{\ge (m+n)\int_0^1f(x)dx}.\end{align}\right)$
- Cute Exercise by Dorin Marghidanu $\left(\displaystyle \sum_{k=1}^n\frac{2k-1}{\sqrt[2k-1]{a_k}}\ge\frac{n^2}{\sqrt[n^2]{a_1a_2\ldots a_n}}\right)$
- A Little of Algebra for an Inequality, A Little of Calculus for a Generalization $\left(\displaystyle \frac{a^{n+1}-b^{n+1}}{a-b}\cdot\frac{b^{n+1}-c^{n+1}}{b-c}\cdot\frac{c^{n+1}-a^{n+1}}{c-a}\gt (n+1)^3(abc)^n\right)$
- An Inequality with Central Binomials $\left(\displaystyle \sqrt{2}\le\sqrt[n(n+1)]{{2\choose 1}{4\choose 2}\cdots{2k\choose k}\cdots{2n\choose n}}\lt 2\right)$
- A Simple Inequality with Many Variables $\left(\displaystyle \sum_{k=1}^n\sqrt{\frac{a_k+a_{k+1}}{a_{k+2}}}\ge n\sqrt{2}\right)$
- Cyclic Inequality in Four Variables $\left(\displaystyle \frac{3}{4}\sum_{cycl}\frac{a^3}{bcd}\ge 1+\frac{\displaystyle 3\sum_{cycl}a^2}{\displaystyle \sum_{all}ab}\right)$
- Cyclic Inequality in Four Variables By D. Sitaru $\left(\displaystyle \sum_{cycl}\frac{a^7}{a^3+bcd}\ge 2abcd\right)$
- Lorian Saceanu's Inequality with Many Variables $\left(\displaystyle \frac{1}{2}\left(\sqrt{ab}+\frac{1}{\sqrt{ab}}\right)\left(\sum_{i=1}^na_kb_k\right)\ge\sqrt{\left(\sum_{i=1}^na_k^2\right)\left(\sum_{i=1}^nb_k^2\right)}\right)$
- A True Algebraic-Geometric Inequality $\left(\displaystyle \small{\sqrt{\sum_{k=1}^n(2a_k-b_k)^2}+\sqrt{\sum_{k=1}^n(2b_k-a_k)^2}\ge\sqrt{\sum_{k=1}^na_k^2}+\sqrt{\sum_{k=1}^nb_k^2}}\right).$
- Leo Giugiuc's Cyclic Inequality in Square Roots $\left(\displaystyle \sqrt{x+y}+\sqrt{y+z}+\sqrt{z+x}\ge 2\sqrt{\frac{(x+y)(y+z)(z+x)}{xy+yz+zx}}\right)$
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73550216
