An Inequality in Reciprocals II
Problem
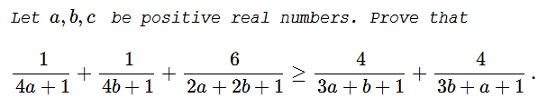
Solution 1
Set $x=4a+1\ge 1,\,$ $y=4b+1\ge 1,\,$ $x+y=2(2a+2b+1).\,$ Further,
$\begin{align} 12a+4b+4 &= 3(4a+1)+(4b+1)=3x+y,\\ 12b+4a+4 &= 3(4b+1)+(4a+1)=3y+x.\\ \end{align}$
We have to prove that
$\displaystyle\frac{1}{x}+\frac{1}{y}+\frac{12}{x+y}\ge\frac{16}{3x+y}+\frac{16}{3y+x}.$
This is the same as $\displaystyle\frac{(x+y)^2+12xy}{xy(x+y)}\ge\frac{64(x+y)}{(3x+y)(3y+x)},\,$ or
$\displaystyle\frac{(x+y)^2+12xy}{xy(x+y)}\ge\frac{64(x+y)}{3x^2+3y^2+10xy}.$
Multiplying out, expanding, and eliminating like terms, we reduce the latter to $(x-y)^4\ge 0,\,$ which is obviously true. Equality is achieved for $x=y,\,$ i.e., $a=b.$
Solution 2
The required inequality is equivalent to an inequality in integrals:
$\displaystyle\begin{align}\int_{0}^{1}x^{4a}dx+\int_{0}^{1}x^{4b}dx&+6\int_{0}^{1}x^{2(a+b)}dx\\ &\ge 4\int_{0}^{1}x^{3a+b}dx+4\int_{0}^{1}x^{3b+a}dx, \end{align}$
which can be rewritten (now without the integrals) as
$A^4+b^4+6A^2B^2\ge4AB(A^2+B^2),$
or, equivalently,
$(A^2+B^2)^2-4AB(A^2+B^2)+4A^2B^2\ge 0,$
i.e., $(A-B)^4\ge 0,\,$ which is true.
Solution 3
The required inequality is equivalent to
$\displaystyle\int_{0}^{1}(t^{4a}+t^{4b}+6t^{2(a+b)})dt\ge 4\int_{0}^{1}(t^{3a+b}+t^{3b+a})dt.$
By letting $x=t^a\,$ and $y=t^b\,$ this reduces to $x^4+y^4+6x^2y^2\ge 4xy(x^2+y^2),\,$ or $(x-y)^4\ge 0.$
Solution 4
Let $A=\displaystyle\frac{1}{4a+1} + \frac{3}{2a+2b+1}-\frac{4}{3a+b+1},\,$ $B=\displaystyle\frac{1}{4b+1} + \frac{3}{2a+2b+1}-\frac{4}{3b+a+1}.\,$ We find
$\displaystyle\begin{align} A&=\frac{2(a-b)(5a-b-1)}{(4a+1)(3a+b+1)(2a+2b+1)},\\ B&=\frac{2(a-b)(a-5b-1)}{(4b+1)(3b+a+1)(2a+2b+1)} \end{align}$
such that
$\displaystyle\begin{align} A+B &= \frac{2(a-b)}{2a+2b+1}\left(\frac{5a-b-1}{(4a+1)(3a+b+1)}+\frac{a-5b-1}{(4b+1)(3b+a+1)}\right)\\ &=\frac{24(a-b)^{4}}{D}, \end{align}$
where $D=(4a+1)(4b+1)(3a+b+1)(a+3b+1)(2a+2b+1).\;$ Clearly $A+B\ge 0.\,$ Equality is achieved when $a=b.$
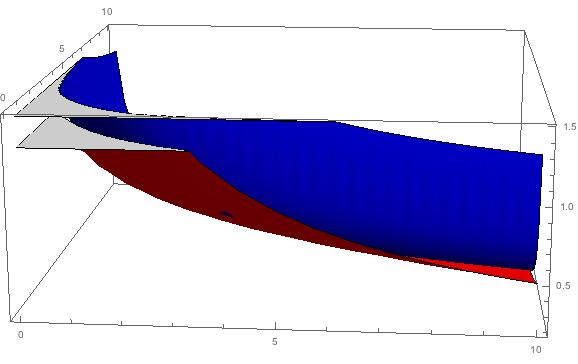
Illustration
LHS in blue, RHS in red.
Acknowledgment
Dan Sitaru has kindly communicated to me the above problem, along with three solution. This is problem JP032 from the Romanian Mathematical Magazine, where it accumulated four solutions. I reproduce these here. The inequality is an invention of Hung Nguyen Viet (Vietnam). Solution 1 is by Kevin Soto Palacios (Peru); Solution 2 is by Soumitra Mandal (India); Solution 3 is by Henry Ricardo (USA); Solution 4 is by Imad Zak (Lebanon). The illustration is by Gary Davis.
- Schur's Inequality $(x^t(x-y)(x-z)+y^t(y-z)(y-x)+z^t(z-x)(z-y)\ge 0)$
- An Application of Schur's Inequality $\small{\left(5\left(\sum\sqrt{x+y}\right)\left(\sum\sqrt{(x+y)(y+z)}\right)\ge\left(\sum\sqrt{x+y}\right)^3+18\sqrt{(x+y)(y+z)(z+x)}\right)}$
- Powers and Fractions Inequality $\left(\displaystyle\sum_{cycl}\frac{a^3b^3}{c^5}\ge \sum_{cycl}\frac{ab}{c}\right)$
- Three Junior Problems from Vietnam $\left(\left(\begin{array}{ccc}0&y&z\\x&0&z\\x&y&0\end{array}\right)\left(\begin{array}\;a\\b\\c\end{array}\right)=\left(\begin{array}\;x\\y\\z\end{array}\right)\right)$
- Newton's and Maclaurin's Inequalities $\left(E_k(X)\right)^2\gt E_{k-1}(X)E_{k+1}(X),$ $\left(\left(E_k(X)\right)^2\gt E_{k-1}(X)E_{k+1}(X)\right)$
- Rearrangement Inequality $\left(\displaystyle\sum_{i=1}^{n}x_iy_{n+1-i}\le\sum_{i=1}^{n}x_iy_{\sigma(i)}\le\sum_{i=1}^{n}x_iy_i\right)$
- Chebyshev Inequality $\left(\displaystyle n\sum_{i=1}^{n}x_iy_{i}\ge\sum_{i=1}^{n}x_i\sum_{i=1}^{n}y_i\right)$
- Chebyshev Holds a Key $\left(\displaystyle\sum_{k=1}^n\left[\left(\sum_{i=1}^k\sin a_i\right)\left(\sum_{i=1}^k\cos a_i\right)\right]\le\frac{n(n+1)(2n+1)}{12}\right)$
- Jensen's Inequality $\left( f(\lambda x_1+(1-\lambda )x_2)\le \lambda f(x_1)+(1-\lambda )f(x_2)\right)$
- Muirhead's Inequality $\left(\mathbf{a}\succ\mathbf{b}\;\right)$ implies $\left([\mathbf{a}]\ge [\mathbf{b}]\right)$
- Bergström's inequality $\left(\displaystyle \frac{x_1^2}{a_1}+\frac{x_2^2}{a_2}+\cdots+\frac{x_n^2}{a_n}\ge\frac{(x_1+x_2+\cdots+x_n)^2}{a_1+a_2+\cdots+a_n}\right)$
- Dorin Marghidanu's Example II $\left(\displaystyle \sum_{k=1}^n\frac{a^2_k}{a_{\sigma(k)}-1}\ge 4n\right)$
- Radon's Inequality and Applications $\left(\displaystyle \frac{x_1^{p+1}}{a_1^p}+\frac{x_2^{p+1}}{a_2^p}+\cdots+\frac{x_n^{p+1}}{a_n^p}\ge\frac{(x_1+x_2+\cdots+x_n)^{p+1}}{(a_1+a_2+\cdots+a_n)^p}\right)$
- Dorin Marghidanu's Example for Radon's Inequality $\left(\displaystyle\frac{a^{m+n+1}}{b^mc^n}+\frac{b^{m+n+1}}{c^ma^n}+\frac{c^{m+n+1}}{a^mb^n}\ge a+b+c\right)$
- Jordan and Kober Inequalities, PWW $\left(\displaystyle x\in\left(0,\frac{\pi}{2}\right)\,\Longrightarrow\,\sin x\gt\frac{2x}{\pi}\right)$
- A Mathematical Rabbit out of an Algebraic Hat $\left(x^{2} + y^{2} + z^{2} - xy - yz - zx \ge 0\right)$
- An Inequality With an Infinite Series $\left(\displaystyle \sum_{n=1}^{1000}\frac{1}{n^{3}+3n^{2}+2n} \lt \frac{1}{4}\right)$
- An Inequality: $\left(1/2 \cdot 3/4 \cdot 5/6 \cdot \ldots \cdot 99/100 \lt 1/10\right)$
- $\left(\text{A Low Bound for }1/2 \cdot 3/4 \cdot 5/6 \cdot \ldots \cdot (2n-1)/2n\right)$
- An Inequality: Easier to prove a subtler inequality
- Inequality with Logarithms (logπ3 + log3π > 2)
- An inequality: 1 + 1/4 + 1/9 + ... less than 2
- Inequality with Harmonic Differences $\left(\displaystyle\frac{2n}{3n+1} \lt \frac{1}{n+1}+\frac{1}{n+2}+\ldots +\frac{1}{n+n}\lt \frac{25}{36}\right)$
- An Inequality by Uncommon Induction $\left(\displaystyle 1+\frac{1}{2^2}+\frac{1}{3^2}+\ldots +\frac{1}{n^2}\gt \frac{3n}{2n+1}\right)$
- Hlawka's Inequality $\left(|x+y|+|y+z|+|z+x|\le |x|+|y|+|z|+|x+y+z|\right)$
- An Application of Hlawka's Inequality $\left(\sqrt{a^2-ab+b^2}+\sqrt{b^2-bc+c^2}+\sqrt{c^2-ca+a^2}\le a+b+c+\sqrt{a^2+b^2+c^2-ab-bc-ca}\right)$
- An Application of Hlawka's Inequality II $\left(\displaystyle xPA+yPB+zPC+\frac{a\sqrt{3}}{2}PM\ge (y+z)PA'+(z+x)PB'+(x+y)PC'\right)$
- Geometric Proof of Hlawka's Inequality $\left(|\vec{a}|+|\vec{b}|+|\vec{c}|+|\vec{d}|\ge |\vec{a}+\vec{d}|+|\vec{b}+\vec{d}|+|\vec{c}+\vec{d}|\right)$
- Hlawka-like Dinca's Inequality $\left((x+y)^{\alpha}+(y+z)^{\alpha}+(z+x)^{\alpha}\le x^{\alpha}+y^{\alpha}+z^{\alpha}+(x+y+z)^{\alpha}\right)$
- Hlawka-like Inequality for Convex Functions $\left(g(x) + g(y) + g(z) + g(x + y + z) \ge g(x + y) + g(x + z) + g(y + z)\right)$
- Hlawka in Convex Quadrilateral $\left(AB+BC+CD+DA\gt AC+BD+2EF\right)$
- Quadrilateral Inequality
- Problem 4165 from Crux Mathematicorum $\left(\displaystyle \left|\sum_{i=1}^4x_i\right|+2\sum_{i=1}^4|x_i|\ge 6\sqrt[6]{\prod_{1\le i\lt j\le 4}|x_i+x_j|}\right)$
- An Inequality in Determinants $\left(\left|\begin{array}{ccc} 1 & 1 & 1\\ a & b & c\\ a^4 & b^4 & c^4\\ \end{array}\right|\ge \left|\begin{array}{ccc} 1 & 1 & 1\\ a & b & c\\ a^3 & b^3 & c^3. \end{array}\right|\right)$
- Application of Cauchy-Schwarz Inequality $\left(\displaystyle\sqrt{a^2-1}+\sqrt{b^2-1}+\sqrt{c^2-1}\le\frac{ab+bc+ca}{2}\right)$
- An Inequality from Tibet $\left((bcde+acde+abde+abce+abcd)^4\ge 125(a+b+c+d+e)(abcde)^3\right)$
- An Inequality from Morocco $\left(\displaystyle 4|(a-b)(b-c)(c-d)(d-a)|\le abcd\right)$
- An Inequality for Mixed Means $\small{\left(\displaystyle \sqrt[m]{\prod_{j=1}^{m}\left[a_j+\frac{1}{n}\sum_{i=1}^{n}x_i\right]}\ge\frac{1}{n}\sum_{i=1}^{n}\sqrt[m]{\prod_{j=1}^{m}(a_j+x_i)} \ge\prod_{i=1}^{n}\prod_{j=1}^{m}\sqrt[mn]{a_j+x_i}\right)}$
- An Inequality in Integers $\left(\displaystyle\frac{a}{b}+\frac{1}{ab}\lt\sqrt{7}\right)$
- An Inequality in Integers II $\left(\displaystyle\frac{a^3+b^3+c^3}{3}-abc\ge 3k\right)$
- An Inequality in Integers III $\left(\displaystyle\sum_{i,j=1}^n \frac{i^2j^2}{i+j-1}\gt n^3\right)$
- An Inequality with Exponents $\left(\displaystyle e^{\frac{4}{e}}\left(b\cdot a^{2\sqrt{a}}+c\cdot b^{2\sqrt{b}}+a\cdot c^{2\sqrt{c}}\right)\ge 3\sqrt[3]{abc}\right)$
- Exponential Inequalities for Means $\left(\displaystyle A_n^{G_nH_n}\le G_n^{A_nH_h}\le H_n^{A_nG_n}\right)$
- A Simple Inequality in Three Variables $\left(\displaystyle\sum_{cyc}ac\left(\frac{1}{2a+b}+\frac{1}{2c+b}\right)\le \sqrt{3(a^2+b^2+c^2)}\right)$
- An Asymmetric Inequality $\left((a+b)(a+c)\ge 2\sqrt{abc(a+b+c)}\right)$
- Linear Algebra Tools for Proving Inequalities $\left(\displaystyle\left(\frac{a}{b-c}\right)^2+\left(\frac{b}{c-a}\right)^2+\left(\frac{c}{a-b}\right)^2\ge 2.\right)$
- An Inequality with a Generic Proof $\left(2\sqrt{b}+\sqrt{aS+b}\le \sqrt{ax+b}+ \sqrt{ay+b}+ \sqrt{az+b}\le \sqrt{3aS+9b}\right)$
- A Generalization of an Inequality from a Romanian Olympiad $\left(\displaystyle \frac{2}{n-1}\sum_{1\le i\lt j\le n}a_{i}a_{j}\le\ln\left(\prod_{k=1}^{n}a_{k}^{a_{k}}\right)+\frac{1}{e}\sum_{k=1}^{n}e^{a_{k}}\right)$
- Area Inequality in Trapezoid $\left([PQRS]\le\frac{1}{4}[ABCD]\right)$
- Improving an Inequality $\left(\displaystyle\sum_{k=1}^{n}\frac{1}{\sqrt{k}}\gt 2(\sqrt{n+1}-1)\right)$
- RomanoNorwegian Inequality $\left(\sqrt{\cot A} + \sqrt{\cot B} + \sqrt{\cot C} \ge 2\right)$
- Inequality with Nested Radicals II $\left(\displaystyle\sqrt{n+1}\le\sqrt{n+\sqrt{(n-1)+\sqrt{\ldots+\sqrt{2+\sqrt{1}}}}}\le\sqrt{2n-1}\right)$
- Inequality with Powers And Radicals $\left(\displaystyle\sum_{cycl}\sqrt[6]{ab^2c^3}\ge\sum_{cycl}\sqrt[30]{a^9b^{10}c^{11}}\right)$
- Inequality with Two Minima $\left(\displaystyle\sqrt{a-c}+\sqrt{b-c}\le\min \left\{\sqrt{\frac{ab}{c}},\sqrt{2(a+b-2c)} \right\}\right)$
- Simple Inequality with Many Faces And Variables $\left(\displaystyle \frac{a^2}{c-1}+\frac{b^2}{d-1}+\frac{c^2}{e-1}+\frac{d^2}{a-1}+\frac{e^2}{b-1}\ge 20\right)$
- An Inequality with Determinants $\left(\displaystyle\left|\begin{array}{cccc}\,a&-b&0&0\\0&b&-c&0\\0&0&c&-d\\1&1&1&1+d\end{array}\right|\ge 3\sqrt[3]{4}(abcd)^{5/6}\right)$
- An Inequality with Determinants II $\left(\displaystyle \Delta=\left|\begin{array}{cccc} \,1 & 1 & 1 & 1\\ a & b & c & d\\ a^2 & b^2 & c^2 & d^2\\ \frac{1}{a^2} & \frac{1}{b^2} & \frac{1}{c^2} & \frac{1}{d^2} \end{array}\right|\lt \frac{1}{abcd}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}\right)\right)$
- An Inequality with Determinants III $\left(\displaystyle \left|\begin{array}{ccccc} \,0 & x^2 & y^2 & z^2 & 1\\ x^2 & 0 & x^2+y^2 & x^2+z^2 & 1\\ y^2 & x^2+y^2 & 0 & y^2+z^2 & 1\\ z^2 & x^2+z^2 & y^2+z^2 & 0 & 1\\ 1 & 1 & 1 & 1 & 0\end{array}\right|\le \left|\begin{array}{ccccc} \,0 & a^2 & b^2 & c^2 & 1\\ a^2 & 0 & a^2+b^2 & a^2+c^2 & 1\\ b^2 & a^2+b^2 & 0 & b^2+c^2 & 1\\ c^2 & a^2+c^2 & b^2+c^2 & 0 & 1\\ 1 & 1 & 1 & 1 & 0\end{array}\right|\right)$
- An Inequality with Determinants IV $\left(\displaystyle\left|\begin{array}{cccc}\,a&-b&0&0\\0&b&-c&0\\0&0&c&-d\\1&1&1&1+d\end{array}\right|\ge 3\sqrt[3]{4}(abcd)^{5/6}\right)$
- An Inequality with Determinants V $\left(\displaystyle \Delta =\left|\begin{array}{cccc} \,s & \frac{a^2b}{a^3+b} & \frac{b^2c}{b^3+c} & \frac{c^2a}{c^3+a}\\ \frac{a^2b}{a^3+b} & s & \frac{c^2a}{c^3+a} & \frac{b^2c}{b^3+c}\\ \frac{b^2c}{b^3+c} & \frac{c^2a}{c^3+a} & s & \frac{a^2b}{a^3+b}\\ \frac{c^2a}{c^3+a} & \frac{b^2c}{b^3+c} & \frac{a^2b}{a^3+b} & s\end{array}\right|\ge 0\right)$
- An Inequality with Determinants VI $\left(\displaystyle\frac{\Delta_1-\Delta_2}{(b-a)(a-c)(b-c)}\ge 12\sqrt[6]{(abc)^5}\right)$
- An Inequality with Determinants VII $\left(\displaystyle \left|\begin{array}{ccccc} \,0 & a^2 & b^2 & c^2 & 1\\ a^2 & 0 & a^2+b^2 & a^2+c^2 & 1\\ b^2 & a^2+b^2 & 0 & b^2+c^2 & 1\\ c^2 & a^2+c^2 & b^2+c^2 & 0 & 1\\ 1 & 1 & 1 & 1 & 0\end{array}\right| \le\frac{1}{8}\prod_{cycl}(a+b)^2\right)$
- An Inequality in Reciprocals $\left(\displaystyle\begin{align}\frac{4}{9}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)&+4\left(\frac{1}{a+2b}+\frac{1}{b+2c}+\frac{1}{c+2a}\right)\\ &\ge 5\left(\frac{1}{2a+b}+\frac{1}{2b+c}+\frac{1}{2c+a}\right)+\frac{1}{a+b+c}. \end{align}\right)$
- An Inequality in Reciprocals II $\left(\displaystyle \frac{1}{4a+1} + \frac{1}{4b+1} + \frac{6}{2a+2b+1} \ge \frac{4}{3a+b+1} + \frac{4}{3b+a+1}\right)$
- An Inequality in Reciprocals III $\left(\displaystyle \frac{1}{3}\sum_{cycl}\frac{1}{a+b} + \sum_{cycl}\frac{1}{4a+b+c}\ge\sum_{cycl}\left(\frac{1}{a+2b+3c}+\frac{1}{a+3b+2c}\right)\right)$
- A Problem from the Danubius Contest 2016 $\left(\displaystyle\{E(a,b)|\;a\gt 0, b\gt 0\}\subset \left(\frac{11}{10},\frac{10}{9}\right]\right)$
- A Problem from the Danubius-XI Contest $\left(\displaystyle\frac{a+b}{(1+c)^2}+\frac{b+c}{(1+a)^2}+\frac{c+a}{(1+b)^2}\ge\frac{9S}{(9+S)^2}\right)$
- An Inequality with Integrals and Rearrangement $\left(\displaystyle \sum_{cycl}b^2c^3\int_0^a(\cot x)(\arctan x)dx\lt abc(a^3+b^3+c^3)\right)$
- An Inequality with Cot, Cos, and Sin $\left(\displaystyle\sum_{cycl}\cot^2A\,\cot^2B\ge\frac{\displaystyle\sum_{cycl}\cos^2A}{\displaystyle\sum_{cycl}\sin^2A}\right)$
- A Trigonometric Inequality from the RMM $\left(\displaystyle\sin (x+y)\le\sin x\left(\frac{\sin y}{y}\right)^3+\sin y\left(\frac{\sin x}{x}\right)^3\right)$
- An Inequality with Finite Sums $\left(\displaystyle\sum_{k=1}^n\frac{(2+x)^k}{2+x\cdot k}\ge 2^n-1\right)$
- Hung Viet's Inequality $\left(\displaystyle 1+\sum_{cycl}\frac{ab}{a^2-ab+b^2}\ge\frac{3}{2}\cdot\frac{(a+b)(b+c)(c+a)}{a^3+b^3+c^3}\right)$
- Hung Viet's Inequality II $\left(\displaystyle\min_{all}(a-b)^2\le\frac{a^2+b^2+c^2+d^2}{5}\right)$
- Hung Viet's Inequality III $\left(\displaystyle \left(\sum_{cycl}a^4\right)\left(\sum_{cycl}ab^3\right)\ge\left(\sum_{cycl}a^3b\right)\left(\sum_{cycl}a^2b^2\right)\right)$
- Inequality by Calculus $\left(\displaystyle\frac{b^{n+1}-a^{n+1}}{n+1}+\frac{ab(b^{n-1}-a^{n-1})}{n-1}\leq (b-a)\sqrt{2(a^{2n}+b^{2n})}\right)$
- Dorin Marghidanu's Calculus Lemma
$\left(\displaystyle u^v\gt\frac{u}{u+v}\right)$
- An Inequality with Exponents from a Calculus Lemma $\left(\displaystyle a^b\cdot (a+b)^c\cdot (a+b+c)^d\gt\frac{a}{a+b+c+d}\right)$
- An Inequality with Exponents from a Calculus Lemma II $\left(2^a(b+c)^{1-a}+2^b(c+a)^{1-b}+2^c(a+b)^{1-c}\lt 4(a+b+c)\right)$
- An Area Inequality $\left(\displaystyle a^{2} + b^{2} + u^{2} + v^{2} + au + bv \ge \frac{3}{2}\right)$
- A 4-variable Inequality from the RMM $\left(\displaystyle |(a-b)(b-c)(c-a)|\le\sum_{cycl}|a-b||a+c+\eta||b+c+\eta|\right)$
- An Inequality from RMM with Powers of 2 $\left(2^x+2^y+2^z+2^{x+y+z}\gt\sqrt[x+y]{16^{xy}}+\sqrt[y+z]{16^{yz}}+\sqrt[z+x]{16^{zx}}+1\right)$
- A Cycling Inequality with Integrals $\bigg(2bc\Omega(a)+2ca\Omega(b)+2ab\Omega(c)\lt a^2+b^2+c^2$ where $\Omega(t)=\displaystyle\int_{0}^{1}\frac{1-x^2}{1+tx^2+x^4}dx\bigg)$
- A Cycling Inequality with Integrals II $\bigg(\Omega(a,b,c)+\Omega(b,c,a)+\Omega(c,a,b)\le 1,$ where $\Omega(p,q,r)=\displaystyle\int_{0}^{1}\frac{x^p}{1+x^p+x^{q+r}}dx\bigg)$
- An Inequality with Absolute Values $\left(\displaystyle\sum_{cycl}\frac{|a|+|b|}{1-c^2} \ge \sum_{cycl}\frac{2|a|}{1-bc}\right)$
- An Inequality from RMM with a Generic 5 $\left(\displaystyle\sqrt[3]{(2a+5)(2b+5)(2c+5)}\ge\frac{6abc}{ab+bc+ca}+5\right)$
- An Elementary Inequality by Non-elementary Means $\left(12(a\sin a + \cos a - 1)^2 \le 2a^4 + a^3\sin 2a\right)$
- Inequality in Quadrilateral $\left(\displaystyle\sum_{cycl}\sqrt{a^2+b^2+c^2}\gt 2\sqrt{3\cdot AC\cdot BD}\right)$
- Marian Dinca's Refinement of Nesbitt's Inequality $\left(\displaystyle\begin{align}\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}&\ge\frac{(a+b+c)^2}{2(ab+bc+ca)}\\&\ge\frac{3\sqrt{3(a^2+b^2+c^2)}}{2(a+b+c)}\\&\ge\frac{3}{2}\end{align}\right)$
- An Inequality in Cyclic Quadrilateral $\left(\displaystyle\frac{R}{8\sqrt{2}}\ge\frac{\sqrt[4]{(abcd)^3}}{(a+b+c+d)^2}\right)$
- An Inequality in Cyclic Quadrilateral II $\left(\displaystyle\sin A\sin B\le (\frac{s}{a}-1)(\frac{s}{b}-1)(\frac{s}{c}-1)(\frac{s}{d}-1)\right)$
- An Inequality in Cyclic Quadrilateral III $\left(\displaystyle\cos\frac{A}{2}\cos\frac{B}{2}\cos\frac{C}{2}\cos\frac{D}{2}\le\frac{S^2}{4abcd}\right)$
- An Inequality in Cyclic Quadrilateral IV $\left(a^2-b^2-c^2+d^2+4S\le 2\sqrt{2}(ad+bc)\right)$
- Inequality with Three Linear Constraints $\left(\displaystyle\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge 1\right)$
- Inequality with Three Numbers, Not All Zero $\left(\displaystyle\frac{a^2-ab+b^2}{b^2+bc+c^2}+\frac{b^2-bc+c^2}{c^2+ca+a^2}+\frac{c^2-ca+a^2}{a^2+ab+b^2}\ge 1\right)$
- An Easy Inequality with Three Integrals $\left(\displaystyle a^2\int_{0}^{b}\frac{\arctan x}{x}dx + b^2\int_{0}^{c}\frac{\arctan x}{x}dx + c^2\int_{0}^{a}\frac{\arctan x}{x}dx \lt a^3+b^3+c^3\right)$
- Divide And Conquer in Cyclic Sums $\left(\displaystyle \sum_{cycl}c\left(\frac{4a}{b^2}+\frac{3b}{a^2}\right)\ge 12+3\sum_{cycl}\frac{a}{b}\right)$
- Wu's Inequality $\left((x^2+xy+y^2)(y^2+yz+z^2)(z^2+zx+x^2)\ge (xy+yz+zx)^3\right)$
- Dorin Marghidanu's Inequality in Complex Plane $\left(\displaystyle \sum_{cycl}(|(2-n)\cdot z_1+z_2+\ldots+z_n|\ge\sum_{k=1}^n|z_k|\right)$
- Dorin Marghidanu's Inequality in Integer Variables $\left(\displaystyle \frac{m}{\sqrt[m]{1+n}}+\frac{n}{\sqrt[n]{1+m}}\gt\frac{m+n}{2}\right)$
- Dorin Marghidanu's Inequality in Many Variables $\left(\displaystyle\prod_{k=1}^{n}\sqrt[n]{\frac{\displaystyle \sum_{i=1,i\ne k}^{k}a_i}{a_k)}} \ge n-1\right)$
- Dorin Marghidanu's Inequality in Many Variables Plus Two More $\left(\displaystyle G_n\left[p+\frac{r}{a_1},p+\frac{r}{a_2},\ldots,p+\frac{r}{a_n}\right]\ge p+\frac{r}{A_n[a_1,a_2,\ldots,a_n]}\right)$
- Dorin Marghidanu's Inequality with Radicals $\left(\displaystyle\sum_{k=1}^{n}\sqrt[i_k]{x_k} \gt \sqrt[\small{\displaystyle \sum_{k=1}^{n}i_k}]{\prod_{k=1}^{n}x_k}\right)$
- Dorin Marghidanu's Light Elegance in Four Variables $\left(\displaystyle \sum_{cycl}(-a+b+c+d)^2\ge 2(a+b+c+d)-1\right)$
- Dorin Marghidanu's Spanish Problem $\left(\displaystyle n^*\le (n_*)^2\right)$
- Two-Sided Inequality - One Provenance $\left(\displaystyle\sum_{k=1}^{2n(n+1)}\frac{1}{\sqrt{2k}+\sqrt{2k+1}}\lt n\lt\sum_{k=1}^{2n(n+1)}\frac{1}{\sqrt{2k-1}+\sqrt{2k}}\right)$
- An Inequality with Factorial $\left(a_1\cdot a_2\cdot\ldots\cdot a_n+(1-a_1)\cdot (2-a_2)\cdot\ldots\cdot (n-a_n)\le n!\right)$
- Wonderful Inequality on Unit Circle $\left(\displaystyle\left(\frac{a+b}{1+ab}\right)^2+\left(\frac{a-b}{1-ab}\right)^2\ge 1\right)$
- Quadratic Function for Solving Inequalities $\left((a^2+3x^2)(b^2+3y^2)(c^2+3z^2)\ge 4(ayz+bzx+cxy+xyz)^2\right)$
- An Inequality Where One Term Is More Equal Than Others $\left(\displaystyle\left(\sum_{k=1}^na_k\right)\left(\sum_{k=1}^n\frac{1}{a_k}\right)\ge n^2+(n-2)^2\right)$
- Complicated Constraint - Simple Inequality $\left(3(a+b)(b+c)(c+a)\ge\frac{\displaystyle 8}{\displaystyle\sqrt[8]{a^3+b^3+c^3}}\right)$
- The power of substitution II: proving an inequality with three variables $\left(\displaystyle\frac{ab}{(a+b)^2}+\frac{bc}{(b+c)^2}+\frac{ca}{(c+a)^2}\le\frac{1}{4}+\frac{4abc}{(a+b)(b+c)(c+a)}\right)$
- Algebraic-Geometric Inequality $\left(\sqrt{x^2-\sqrt{3}xy+y^2} + \sqrt{y^2-\sqrt{2}yz+z^2} \ge \sqrt{z^2-zx+x^2}\right)$
- One Inequality - Two Domains $\left(\displaystyle 3\prod_{cycl}(a^2+ab+b^2)\ge\left(\sum_{cycl}a\right)^2\cdot\left(\sum_{cycl}ab\right)^2\right)$
- Radicals, Radicals, And More Radicals in an Inequality $\bigg(\displaystyle\gamma=\frac{\sqrt[4]{xz}}{\sqrt{x}+\sqrt{z}}.\,$ Prove that $\sqrt{x}+\sqrt{y}+\sqrt{z}\ge 2\gamma\sqrt{3(x+y+z)}\bigg)$
- An Inequality in Triangle and In General $\left(\displaystyle\sum_{cycl}\frac{\cot A\,\cot^3B}{\cot^2B+2\cot^2A}+2\sum_{cycl}\frac{\cot^2A\cot B}{\cot A+2\cot B}\ge 1\right)$
- Dan Sitaru's Cyclic Inequality In Many Variables $\left(\displaystyle a+b+c+d\le \frac{a^5+b^5+c^5+d^5}{abcd}\right)$
- An Inequality on Circumscribed Quadrilateral $\left(s\ge 4R\right)$
- An Inequality with Fractions $\left(\displaystyle m\le\frac{a_1+a_2+\ldots+a_n}{b_1+b_2+\ldots+b_n}\le M\right)$
- An Inequality with Complex Numbers of Unit Length $\left(|a-b|+|a-c|\ge |a+b|+|a+c|\right)$
- An Inequality with Complex Numbers of Unit Length II $\left(|a^2+bc|\ge |b+c|\right)$
- Le Khanh Sy's Problem $\left(xa^2+yb^2+zc^2\ge 2m\right)$
- An Inequality Not in Triangle $\left(\displaystyle\sqrt{a^2+b^2-ab\sqrt{2}}+\sqrt{b^2+c^2-bc\sqrt{3}}+\sqrt{c^2+d^2-\frac{cd(\sqrt{6}+\sqrt{2})}{2}}\ge\sqrt{a^2+d^2}\right)$
- An Acyclic Inequality in Three Variables $\left(\displaystyle \frac{(a^2-bc)^2+(b^2-ca)^2+(c^2-ab)^2}{a^2+b^2+c^2+ab+bc+ca}\geq 3(a-b)(b-c)\right)$
- An Inequality with Areas, Norms, and Complex Numbers $\left(\displaystyle \frac{(ad-bc)(3(a^2+b^2)(c^2+d^2)-4(ad-bc)^2)}{\left((a^2+b^2)(c^2+d^2)\right)^{\frac{3}{2}}}\le 1\right)$
- Darij Grinberg's Inequality In Three Variables $\left(a^2+b^2+c^2+2abc+1\ge 2(ab+bc+ca)\right)$
- Small Change Makes Big Difference $\left(\displaystyle\frac{1}{\displaystyle \sqrt{1+a^2-\frac{(a-b)^2}{2}}}+\frac{1}{\displaystyle \sqrt{1+b^2-\frac{(a-b)^2}{2}}}\ge\frac{2}{\sqrt{1+ab}}\right)$
- Inequality with Two Variables? Think Again $\left(\displaystyle\frac{1}{\sqrt{1+a^2}}+\frac{1}{\sqrt{1+b^2}}\le\frac{2}{\sqrt{1+ab}}\right)$
- A Problem From a Mongolian Olympiad for Grade 11 $\left(\displaystyle \frac{a}{3a+2b^3}+ \frac{b}{3b+2c^3}+ \frac{c}{3c+2a^3}\le\frac{1}{5}\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)\right)$
- Sitaru--Schweitzer Inequality
$\left(\displaystyle \left(\int_{a}^{b}f(x)dx\right)\left(\int_{a}^{b}\frac{1}{f(x)}dx\right)\le\frac{(m+M)^2}{4mM}(b-a)^2\right)$
- Pólya-Szegö Inequality $\left(\displaystyle \frac{\displaystyle \left(\sum_{k=1}^{n}a^2_{k}\right)\left(\sum_{k=1}^{n}b^2_{k}\right)}{\displaystyle\left(\sum_{k=1}^{n}a_{k}b_{k}\right)^2}\le\left(\frac{\displaystyle \sqrt{\frac{M_1M_2}{m_1m_2}}+\sqrt{\frac{m_1m_2}{M_1M_2}}}{2}\right)^2\right)$
- Kantorovich Inequality $\left(\displaystyle \left(\sum_{k=1}^{n}\gamma_ku_k^2\right)\left(\sum_{k=1}^{n}\frac{1}{\gamma_k}u_k^2\right)\le\frac{1}{4}\left(\sqrt{\frac{M}{m}}+\sqrt{\frac{m}{M}}\right)^2\left(\sum_{k=1}^{n}u^2_{k}\right)^2\right)$
- Greub-Rheinboldt Inequality $\left(\displaystyle \left(\sum_{k=1}^{n}a_k^2u_k^2\right)\left(\sum_{k=1}^{n}b_k^2u_k^2\right)\le\frac{(M_1M_2+m_1m_2)^2}{4m_1m_2M_1M_2}\left(\sum_{k=1}^{n}a_kb_ku^2_{k}\right)^2\right)$
- An Inequality with Cyclic Sums And Products $\left(\small{\displaystyle \sum_{cycl}\frac{a^2}{(b+c+d+e)(a-b)(a-c)(a-d)(a-e)}\lt\frac{(a+b+c+d+e)^2}{1024abcde}}\right)$
- Problem 1 From the 2016 Pan-African Math Olympiad $\left(\displaystyle \sum_{cycl}\frac{1}{(x+1)^2+y^2+1}\le\frac{1}{2}\right)$
- An Inequality with Integrals and Radicals $\left(\displaystyle \Bigr(\int_0^1 \sqrt[3]{f(x)}dx\Bigr)\Bigr(\int_0^1 \sqrt[5]{f(x)}dx\Bigr)\Bigr(\int_0^1 \sqrt[7]{f(x)}dx\Bigr)\leq 1\right)$
- Twin Inequalities in Four Variables: Twin 1 $\left(\displaystyle (ac+bd)^2\le\left(b\sqrt[5]{ab^4}+d\sqrt[5]{cd^4}\right)\left(a\sqrt[5]{a^4b}+c\sqrt[5]{c^4d}\right)\right)$
- Twin Inequalities in Four Variables: Twin 2 $\left(\displaystyle (a\sqrt[3]{a^2b}+c\sqrt[3]{c^2d})(b\sqrt[3]{ab^2}+d\sqrt[3]{cd^2})\le (a^2+c^2)(b^2+d^2)\right)$
- Simple Inequality with a Variety of Solutions $\left(\displaystyle \sum_{cycl}\left(\frac{\ln x}{\ln y\ln z}+\frac{\ln y}{\ln z\ln x}\right)\ge\frac{18}{\ln (xyz)}\right)$
- A Partly Cyclic Inequality in Four Variables $\left(\displaystyle \sum_{cycl}xe^x\ge (x+y+2)e^{x+y+2}+(z+t-2)\sqrt[3]{e^{z+t-2}}\right)$
- Dan Sitaru's Inequality by Induction $\left(\displaystyle\begin{align}&\small{\frac{3}{a+1}+\frac{3}{b+1}+\frac{2}{c+1}+\frac{1}{d+1}}\\ &\small{\qquad\le 6+\frac{1}{a+b+1}+\frac{1}{a+b+c+1}+\frac{1}{a+b+c+d+1}}\end{align}\right)$
- An Inequality in Three (Or Is It Two) Variables $\left(\displaystyle \frac{(x+y)^2}{(x\sin^2z+y\cos^2z)(x\cos^2z+y\sin^2z)}+\frac{x}{y}+\frac{y}{x}\geq 6\right)$
- An Inequality in Four Weighted Variables $\left(\displaystyle (a+c)^c(b+d)^d(c+d)^{c+d}\le c^cd^d(a+b+c+d)^{c+d}\right)$
- An Inequality in Fractions with Absolute Values $\left(\displaystyle \omega\lt\frac{1}{3}\left(\sum_{cycl}\frac{a|a|-b|b|}{a-b}\right)\lt 2\Omega\right)$
- Inequalities with Double And Triple Integrals $\left(\displaystyle \int_0^{\frac{\pi}{2}}\int_0^{\frac{\pi}{2}}\cos\left(\frac{x+y}{2}\right)dxdy\ge\frac{\pi}{2}\right)$
- An Old Inequality $\left(\displaystyle \frac{4ab}{(a+b)^2}\ge\cos\left(\frac{\pi}{2}\cdot\frac{a-b}{a+b}\right)\right)$
- Dan Sitaru's Amazing, Never Ending Inequality $\left(\displaystyle \small{\sum_{cycl}\left(\frac{a}{b}\right)^2\cdot\sum_{cycl}\left(\frac{a}{b}\right)^4\cdot\sum_{cycl}\left(\frac{a}{b}\right)^8\ge\sum_{cycl}\left(\frac{a}{c}\right)\cdot\sum_{cycl}\left(\frac{b}{a}\right)\cdot\sum_{cycl}\left(\frac{b}{c}\right)}\right)$
- Leo Giugiuc's Exercise $\left(\displaystyle x\sin x+x^2\cos x\le 2\sin^2x\right)$
- Another Inequality with Logarithms, But Not Really $\left(\displaystyle \sum_{cycl}\frac{\log_y^3x+\log_z^3y}{\log_y^2x+\log_zx+\log_z^2y}\geq 2\right)$
- An Inequality Solved by Changing Appearances $\left(\displaystyle \sum_{cycl}a^2\cdot\sum_{cycl}\frac{1}{x^2}+\frac{\displaystyle 2\sum_{cycl}ab\cdot\sum_{cycl}x}{xyz}\ge 0\right)$
- Distances to Three Points on a Circle $\left(3\le |z-a|+|z-b|+|z-c|\le 4\right)$
- An Inequality with Powers And Logarithm $\left(\displaystyle \frac{a}{b}+\frac{a^2}{b^2}+\frac{a^3}{b^3}+12\ln b\ge\frac{b}{a}+\frac{b^2}{a^2}+\frac{b^3}{a^3}+12\ln a\right)$
- Four Integrals in One Inequality $\left(\displaystyle \small{\left(\int_a^bxf(x)dx\right)\left(\int_a^bf^2(x)dx\right)\left(\int_a^bx^3f(x)dx\right)\ge\frac{a^2b^2}{b-a}\left(\int_a^bf(x)dx\right)^4}\right)$
- Same Integral, Three Intervals $\left(\displaystyle\small{I(u,v)=\int_u^v\left(\arctan\left(\frac{u\sin x}{v+u\cos x}\right)+\arctan\left(\frac{v\sin x}{u+v\cos x}\right)\right)dx}\right)$
- Dorin Marghidanu's Inequality with Generalization $\left(\displaystyle (x+y)^2+(y+z)^2+(z+x)^2+12ab\le 4(a+b)(x+y+z)\right)$
- Dan Sitaru's Inequality with Three Related Integrals and Derivatives $\left(\displaystyle\small{\left(\int_0^af(x)dx\right)^4\leq \frac{a^8}{60}\left(\int_0^a \left(f'(x)\right)^2 dx\right)\left(\int_0^a \left(f''(x)\right)^2dx\right)}\right)$
- An Inequality in Two Or More Variables $\left(\displaystyle \frac{a}{1+a}+\frac{b}{(1+a)(1+b)}+\frac{c}{(1+a)(1+b)(1+c)}\geq \frac{7}{8}\right)$
- An Inequality in Two Or More Variables II $\left(\displaystyle (a+1)^{a+1}\cdot (b+1)^{b+1}\cdot (c+1)^{c+1}\le e^{a+b+c}\cdot\sqrt{e^{a^2+b^2+c^2}}\right)$
- A Not Quite Cyclic Inequality $\left(\displaystyle \frac{a^2+b^2+c^2}{a+b+c} \le \frac{ab+bc+ca}{a+b+c} + |a-b|+|b-c|\right)$
- Dan Sitaru's Inequality: From Three Variables to Many in Two Ways $\left(\displaystyle a+b+c\ge\frac{3}{2}\right)$
- An Inequality with Sines But Not in a Triangle $\left(\displaystyle \prod_{cycl}\Bigr(a^2\sin \frac{2\pi}{a}+(a+1)^2\sin \frac{2\pi}{a+1}\Bigr)\gt 2^{16}\right)$
- An Inequality with Angles and Integers $\left(\displaystyle k^2\tan \alpha +l^2\tan \beta \geq \frac{2kl}{\sin (\alpha+\beta)}-(k^2+l^2)\cot (\alpha+\beta)\right)$
- Sladjan Stankovik's Inequality In Four Variables $\left(\displaystyle 2\sum_{cycl}a^2-3\frac{\displaystyle \sum_{cycl}a^3}{\displaystyle \sum_{cycl}a}\le\sum_{all}ab\right)$
- An Inequality with Two Pairs of Triplets $\left(\displaystyle (a^2+b^2+c^2)\left(\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}\right)+\frac{2(ab+bc+ca)(x+y+z)}{xyz}\ge 0\right)$
- A Refinement of Turkevich's Inequality $\left(\displaystyle a^2+b^2+c^2+d^2+\frac{32abcd}{(a+b+c+d)^2}\ge \sum_{sym}ab\right)$
- Dan Sitaru's Exercise with Pi and Ln $\left(\displaystyle \small{\arctan(z-x)+\arctan(z-y)+\arctan(y-x) \lt \frac{\pi}{2} - \ln(2)}\right)$
- Leo Giugiuc's Cyclic Quickie in Four Variables $\left(3(xyz+yzt+ztx+txy)^2\ge 8(xy+xz+xt+yz+yz+zt)xyzt\right)$
- Dan Sitaru's Cyclic Inequality in Four Variables $\left(\displaystyle \sum_{cycl}\frac{a^7}{bcd+a^3}\ge 2abcd\right)$
- A Not Quite Cyclic Inequality from Tibet $\left((x+y)^2(z^2+xz+x^2+xy+y^2+yz)^2\ge 8(xy+yz+zx)^2(x^2+y^2)\right)$
- An inequality in 2+2 variables from SSMA magazine $\left(\displaystyle k^2\tan\alpha+l^2\tan\beta\ge\frac{2kl}{\sin (\alpha+\beta)}-(k^2+l^2)\cot(\alpha+\beta)\right)$
- Kunihiko Chikaya's Inequality with Parameter $\bigg(p \ge 2.$ Prove $\displaystyle \sum_{cycl}\frac{a}{\sqrt{ap+b}} \le \sqrt{\frac{3(a+b+c)}{p+1}}\bigg)$
- Dorin Marghidanu's Permuted Inequality $\left(\displaystyle \sum_{k=1}^n\left(a_k+\frac{1}{a_{\sigma(k)}}\right)^p\ge \frac{(s^2+n^2)^p}{n^{p-1}s^p}\right)$
- An Inequality Involving Arithmetic And Geometric Means $\left(\displaystyle\sum_{cycl}\frac{1}{a^4+b^4+c^4+abcd}\le \frac{1}{abcd}\right)$
- Dorin Marghidanu's Sums and Products $\left(\displaystyle \sum_{k=1}^n\frac{a_k}{P_kS_k}\ge\frac{n^n}{\displaystyle (n-1)S^{n-1}}\right)$
- Simple Nameless Inequality $\left(\displaystyle \sum_{k=1}^n\frac{S}{S_k}\ge\frac{n^2}{n-1}\right)$
- Volume Inequality in Tetrahedron $\left(OA\cdot OB\cdot OC\ge 27xyz\right)$
- Inequality in Convex Quadrilateral $\left(\displaystyle\frac{\displaystyle \sum_{cycl}\sqrt{b+c+d-a}}{a+b+c+d}\ge\sqrt{\frac{2(a+b+c+d)}{a^2+b^2+c^2+d^2}}\right)$
- Dan Sitaru's Inequality with a Double Integral $\left(\displaystyle\begin{align}&\small{\int_0^1\int_0^1\sqrt{\left(m^2\sqrt{mnf(x)f(y)}+f^2(x)\right)\left(n^2\sqrt{mnf(x)f(y)}+f^2(y)\right)}dxdy}\\ &\qquad\qquad\qquad\qquad\small{\ge (m+n)\int_0^1f(x)dx}.\end{align}\right)$
- Cute Exercise by Dorin Marghidanu $\left(\displaystyle \sum_{k=1}^n\frac{2k-1}{\sqrt[2k-1]{a_k}}\ge\frac{n^2}{\sqrt[n^2]{a_1a_2\ldots a_n}}\right)$
- A Little of Algebra for an Inequality, A Little of Calculus for a Generalization $\left(\displaystyle \frac{a^{n+1}-b^{n+1}}{a-b}\cdot\frac{b^{n+1}-c^{n+1}}{b-c}\cdot\frac{c^{n+1}-a^{n+1}}{c-a}\gt (n+1)^3(abc)^n\right)$
- An Inequality with Central Binomials $\left(\displaystyle \sqrt{2}\le\sqrt[n(n+1)]{{2\choose 1}{4\choose 2}\cdots{2k\choose k}\cdots{2n\choose n}}\lt 2\right)$
- A Simple Inequality with Many Variables $\left(\displaystyle \sum_{k=1}^n\sqrt{\frac{a_k+a_{k+1}}{a_{k+2}}}\ge n\sqrt{2}\right)$
- Cyclic Inequality in Four Variables $\left(\displaystyle \frac{3}{4}\sum_{cycl}\frac{a^3}{bcd}\ge 1+\frac{\displaystyle 3\sum_{cycl}a^2}{\displaystyle \sum_{all}ab}\right)$
- Cyclic Inequality in Four Variables By D. Sitaru $\left(\displaystyle \sum_{cycl}\frac{a^7}{a^3+bcd}\ge 2abcd\right)$
- Lorian Saceanu's Inequality with Many Variables $\left(\displaystyle \frac{1}{2}\left(\sqrt{ab}+\frac{1}{\sqrt{ab}}\right)\left(\sum_{i=1}^na_kb_k\right)\ge\sqrt{\left(\sum_{i=1}^na_k^2\right)\left(\sum_{i=1}^nb_k^2\right)}\right)$
- A True Algebraic-Geometric Inequality $\left(\displaystyle \small{\sqrt{\sum_{k=1}^n(2a_k-b_k)^2}+\sqrt{\sum_{k=1}^n(2b_k-a_k)^2}\ge\sqrt{\sum_{k=1}^na_k^2}+\sqrt{\sum_{k=1}^nb_k^2}}\right).$
- Leo Giugiuc's Cyclic Inequality in Square Roots $\left(\displaystyle \sqrt{x+y}+\sqrt{y+z}+\sqrt{z+x}\ge 2\sqrt{\frac{(x+y)(y+z)(z+x)}{xy+yz+zx}}\right)$
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny73558971
