Antiparallel and Circumradius
What Might This Be About?
26 January 2016, Created with GeoGebra
Problem
In $\Delta ABC\;$ $MN\;$ is an antiparallel, $M\in AC,\;$ $N\in BC;\;$ $O\;$ the circumcenter.
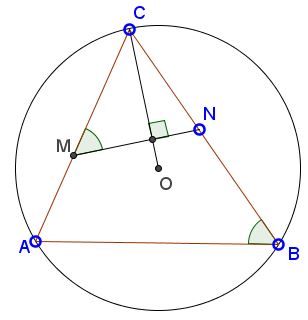
Then $MN\perp OC.$
Proof
Let $B'\;$ be the midpoint of $AC,;$ $D$ the intersection of $MN\;$ and $OC.\;$
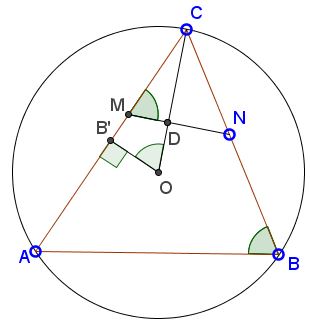
Then triangles $CDM\;$ and $CB'O\;$ are similar. Indeed, they share an angle at $C.\;$ Also, since $AOC$ is a central angle in $(ABC),\;$ $\angle AOC=2\angle ABC,\;$ implying $\angle B'OC=\angle ABC=\angle CDM,\;$ the latter because $MN\;$ is an antiparallel.
So the triangles are similar. $\angle CB'O=90^{\circ},\;$ hence, $\angle CDM=90^{\circ}.$
Remarks
Grégoire Nicollier has observed that the above result is a direct consequence of the fact that circumcenter and orthocenter are isogonal conjugates: when you reflect $\Delta ABC\;$ in the angle bisector of $C,\;$ the altitude through $C\;$ is mapped to the circumdiameter through $C.\;$ In addition, he noted that in a $\Delta ABC,\;$ the bisector of angle $A\;$ and the perpendicular bisector of side $BC\;$ meet on the circumcircle (an immediate consequence of the inscribed angle theorem.)
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578286
