Antiparallel via Three Reflections
What Is It About?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Antiparallel via Three Reflections

The applet illustrates a problem from the College Mathematical Journal (909, by Francisco Javier García Capitán, Spain)

Let α, β, γ be the angular measures of angles BAC, ABC, ACB: α + β + γ = 180°. We chase the angles: in ΔABL,

∠ALB = 180° - α/2 - β = γ + α/2.

Since D is the reflection of L in X (IX⊥BC), ∠IDL = γ + α/2. Also

∠IDB = 180° - (γ + α/2) = β + α.

Next, by the two reflections in BI and CI,

∠AB'I = ∠IDL = γ + α/2 and
∠AC'I = ∠IDB = β + α/2.

It follows that ∠AB'I + ∠AC'I = α + β + γ = 180°, making quadrilateral AB'IC' cyclic.

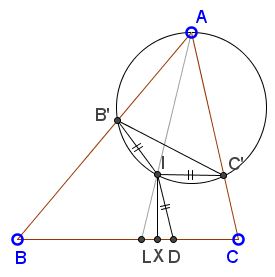
From here, ∠B'IC' = 180° - alpha; and, since ΔB'IC' is isosceles,

∠IB'C' = ∠IC'B' = α/2.

Further,

∠AB'C' = ∠AB'I - ∠IB'C' = (γ + α/2) - α/2 = γ.

Similarly, ∠AC'B' = β which makes the line B'C' antiparallel to BC. As we know, this implies that quadrilateral BCC'B' is cyclic.

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny