Geometric/Trigonometric Observation/Exercise
Source
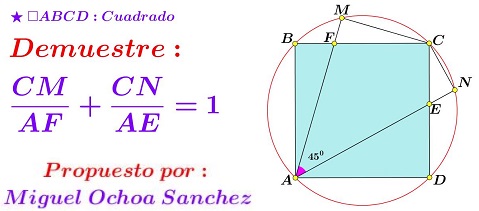
Problem
Let $M\,$ be a point on the minor arc $\overset{\frown}{BC},\,$ of the circumcircle $(ABCD)\,$ of the square $ABCD;\,$ let $N\,$ lie on the minor arc $\overset{\frown}{CD}\,$ such that $\angle MAN=45^{\circ}.\,$
Define $E\,$ and $F\,$ as the intersections of $AN\,$ with $CD\,$ and $AM\,$ with $BC,\,$ respectively. Prove that
$\displaystyle \frac{CM}{AF}+\frac{CN}{AE}=1.$
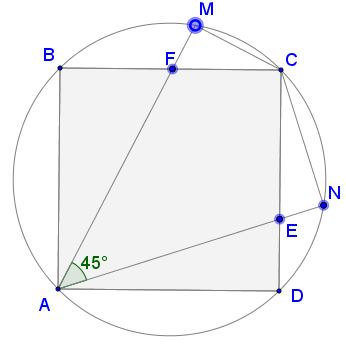
Solution 1
Simple angle chasing shows that $\angle BAF=\angle FCM\,(=\alpha)\,$ and $\angle DAE=\angle ECN\,(=\beta)\,$ and, in addition, $\alpha+\beta=45^{\circ}.$
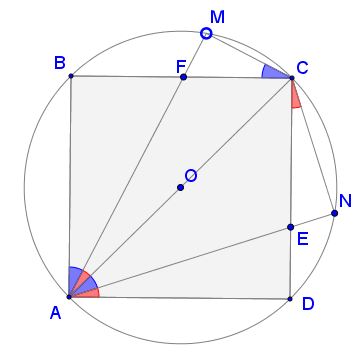
With $AC\,$ being a diameter of $(ABCD),\,$ triangles $ACM\,$ and $ACN\,$ are right. We have
From $\Delta ABF,\,$ $AF=\displaystyle \frac{AB}{\cos\alpha},$
from $\Delta ACM,\,$ $CM=AC\cdot\sin\beta,$
from $\Delta ADE,\,$ $AE=\displaystyle \frac{AD}{\cos\beta},$ and
from $\Delta ACN,\,$ $CN=AC\cdot\sin\alpha.$
Also, $AB=AD\,$ and $AC=\sqrt{2}\cdot AB.\,$ Assume $AB=1.\,$ It follows that
$\displaystyle\begin{align}\frac{CM}{AF}+\frac{CN}{AE}&=\sqrt{2}\cdot\sin\beta\cos\alpha+\sqrt{2}\cdot\sin\alpha\cos\beta\\ &=\sqrt{2}\sin(\alpha+\beta)=\sqrt{2}\sin 45^{\circ}=1. \end{align}$
Solution 2
Let the side of the square be $s$, $\angle CAM=\alpha$ and $\angle CAN=\beta$. Thus, $\beta=45^o-\alpha$, $\angle BAF=45^o-\alpha$ and $\angle AFB=45^o+\alpha.\,$ Applying sine rule to triangles $ACM$ and $AFB$,
$\displaystyle \frac{1}{s\sqrt{2}}=\frac{\sin\alpha}{CM},~\frac{\sin(45^o+\alpha)}{s}=\frac{1}{AF}.$
Dividing one of the the equations by the other and rearranging,
$\displaystyle\begin{align} \frac{CM}{AF}&=\sqrt{2}\sin\alpha\sin(45^o+\alpha)=\sqrt{2}\sin\alpha\cos(45^o-\alpha), \\ \frac{CN}{AE}&=\sqrt{2}\sin\beta\cos(45^o-\beta)=\sqrt{2}\sin(45^o-\alpha)\cos\alpha.~\text{(Analogy)} \end{align}$
Thus,
$\displaystyle \frac{CM}{AF}+\frac{CN}{AE}=\sqrt{2}\left[\sin\alpha\cos(45^o-\alpha)+\sin(45^o-\alpha)\cos\alpha\right]=\sqrt{2}\sin 45^o = 1.$
Solution 3
We shall refer to the following configuration:
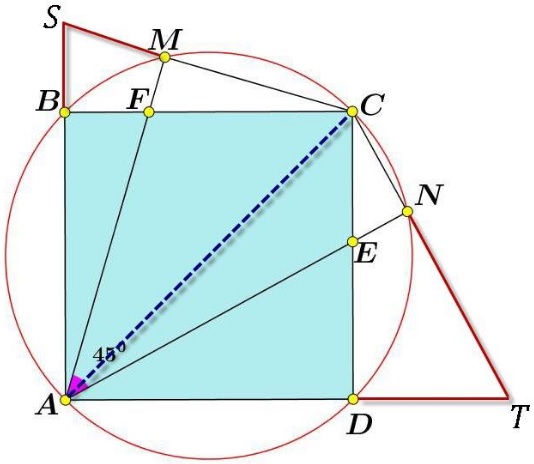
$\Delta ASC\sim\Delta ACT,\,$ hence,
(1)
$\displaystyle \frac{AC}{AT}=\frac{AS}{AC}.$
Further, $\angle SAC=45^{\circ},\,$ $F\,$ is the orthocenter of $\Delta ASC\,$ such that $AF=CS.\,$ Similarly, in $\Delta ACT,\,$ $AE=CT.$
(2)
$\displaystyle\Delta AMC\sim\Delta ANT\;\Rightarrow\;\frac{CM}{AC}=\frac{AE-CN}{AT}$
(3)
$\displaystyle\Delta ANC\sim\Delta AMS\;\Rightarrow\;\frac{CN}{AC}=\frac{AF-CM}{AS}$
(1)-(3) yield
(4)
$\displaystyle\frac{CM}{AE-CN}\frac{AF-CM}{CN}.$
And, after a sequence of calculations,
$AE\cdot CM+AF\cdot CN=AE\cdot AF,$
so that $\displaystyle \frac{CM}{AF}+\frac{CN}{AE}=1.$
Acknowledgment
The above problem has been posted by Miguel Ochoa Sanchez was originally posted at the Peru Geometrico facebook group and appeared on my timeline. Solution 2 is by Amit Itagi; Solution 3 is by Thanos Kalogerakis.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73608846
