Homothety in Equilateral Triangles

Any two circles are homothetic. Let $O$ be the center of homothety that maps the given circle $\omega=(PQRSTU)$ onto the circumcircle $(ABC).$ Let that homothety map $T$ to $T'$ and $U$ to $U'.$

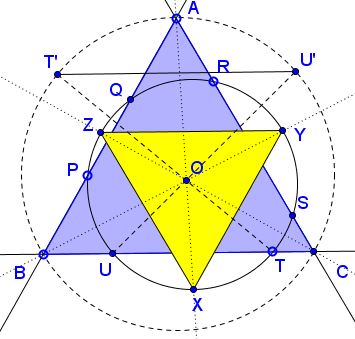
Then $TU\parallel T'U',$ i.e., $BC\parallel T'U'.$ But, $\Delta ABC$ being equilateral, $A$ is the midpoint of the arcs $BC$ and so it is also the midpoint of the arc $T'U'.$ Since homothety preserves angles, the image of $X$ (the midpoint of arc $TU$ of $\omega)$ is the midpoint of arc $T'U'$ of $(ABC)$ which is $A.$ Similarly, $Y$ is mapped on $B$ and $Z$ is mapped on $C.$ The inverse mapping is also a homothety, hence preserves angles, and maps the equilateral $\Delta ABC$ on an equilateral triangle, but the image of $\Delta ABC$ is $\Delta XYZ,$ implying that the latter is also equilateral.

Let $G$ be the center of $\omega:$ $GX=GY=GZ$ and $GX\perp BC,$ $GY\perp AC,$ $GZ\perp AB.$

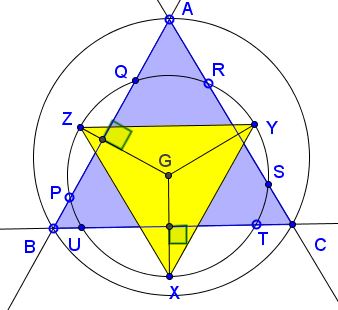
It follows that $\angle XGZ=\angle YGZ=\angle XGY.$ In particular $\angle OXY=\angle OXZ=30^{\circ},$ so that $\angle YXZ=60^{\circ}.$ Similarly, $\angle XYZ=\angle XZY=60^{\circ}.$

The above problem has been posted by Miguel Ochoa Sanchez at the CutTeKnotMath facebook page; the second solution is by Emil Stoyanov; Leo Giugiuc supplied a trigonometric solution.