Yet Another Generalization of Bottema's Theorem

What Might This Be About?

Problem

Given three points $A$, $B,$ $C,$ and angle $\phi.$ Define $C_A$ to be the rotation of $C$ through angle $\phi$ around $A$ and $C_B$ to be the rotation of $C$ through angle $\phi-\pi$ around $B.$ Let $D$ be the midpoint of $C_A$ and $C_B.$ (This means rotating by $\phi$ and $\pi -\phi$ in opposite directions.)

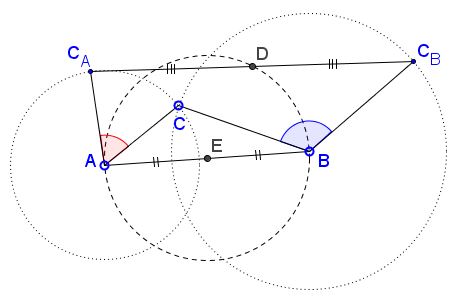
yet another generalization of Bottema's Theorem

Then

$D$ is independent of $C.$
$D$ lies on the circle with diameter $AB,$ and therefore $\angle ADB=90^{\circ}.$

Solution 1

I'll use complex numbers, assuming $A=\alpha,$ $B=\beta,$ $C=\gamma.$ Then

$\begin{align}\displaystyle C_{A}&=\alpha + (\gamma -\alpha)e^{i\phi},\\ C_{B}&=\beta + (\gamma -\beta)e^{i(\phi-\pi)}=\beta - (\gamma -\beta)e^{i\phi} \end{align}$

such that $\displaystyle D=\frac{1}{2}\big(\alpha +\beta +e^{i\phi}(\beta -\alpha)\big)$ - independent of $C(\gamma ).$ This proves the first part, but also the second, because, as $\phi$ changes, $D$ stays on the circle centered at $\displaystyle \frac{\alpha +\beta}{2}$ with radius $\displaystyle \frac{|\beta -\alpha |}{2}.$

Solution 2

A product of rotations is a rotation through the angle which is the sum of the angles of the two consituent rotations. (It could be a translation of the angles ad up to a multiple of $360^{\circ}.)$ If we start working backwards, first rotating $C_B$ to $C$ and then $C$ to $C_A$ we may consider the latter as the image of $C_B$ under the rotation through $180^{\circ}$ which is a central symmetry. The center of that central symmetry depends on the centers of the two rotations but not on the point being rotated and is thus independent of $C_B$ and, therefore, independent from $C.$

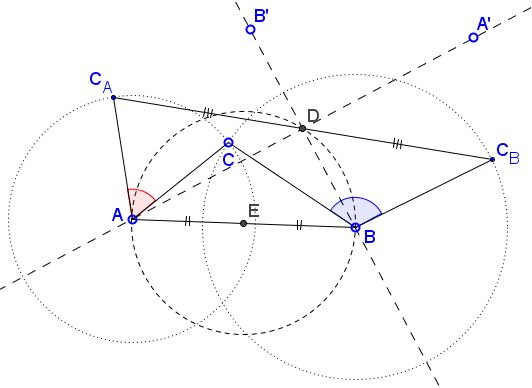
yet another generalization of Bottema's Theorem

If it were not for the Bottema theorem, how would we go about finding point $D?$ I'll do that for the product of two rotations through angles $\alpha$ and $\beta$ around points $A$ and $B,$ respectively. The product of rotations rotates $A$ around $B$ through angle $\beta$ into $A'.$ There is point $B'$ that is brought onto $B$ when rotated around $A$ through angle $\alpha.$ Thus $A'$ is the image of $A$ under the product of two rotations, while $B$ is the image of $B'.$ It follows that the center $D$ of the product of the two rotations lies on the perpendicular bisectors of $AA'$ and $BB'.$ One of these passes through $A,$ the other through $B;$ they meet at $D.$ In triangle $ABD,$ the angle at $A$ is $\alpha /2,$ that at $B$ is $\beta /2.$ the remaining angle at $D$ is therefore $180^{\circ}-(\alpha +\beta )/2$ such that if $\alpha + \beta =180^{\circ}$ then the angle at $D$ is $90^{\circ}.$

Hubert Shutrick offered a shortcut: "$B$ is not moved by the first rotation and goes to $B'$ with the one round $A$ so $BAB'$ is an isosceles triangle with $D$ at the midpoint of $BB'.$"

Acknowledgment

The second solution came up in a discussion with Machó Bónis.

Bottema's Theorem

72203649